平板要素でモデル化してFEM解析を行うと、下記のようなエラーメッセージが表示されて計算できないときがあります。
| Version 3.00.03 |
[4261] Solverエラー :平板要素の行列式が正ではありません。
平板要素の形状等を確認してください。 |
エラーの原因は、平板要素内のプリミティブの形が悪いためです。たとえば、四角形1次要素の場合に図1のような形だと上記エラーが発生します。
 |
| ■図1 計算できない四角形1次要素 |
最も理想的な形は、三角形要素であれば正三角形、四角形要素であれば正方形です。モデル化する上では理想通りにいかないことが多々あると思いますが、計算できた場合であっても正三角形や正方形から形が遠ざかるにつれて得られた解には精度低下の可能性があることにご注意ください。 |
Version 3.01.00 には、平板要素を構成する各プリミティブの形状に異常がないかどうかをチェックする機能が搭載されています。このチェックは、すべてのガウス点においてヤコビ行列の行列式(ヤコビアン)を計算し、ゼロまたは負になっている場合に問題のある平板要素とプリミティブ番号をエラーメッセージ欄に表示します。
| Version 3.01.00 |
[4209] (1) 計算できない平板要素の形があります。大きな内角や
小さな内角は避けてください。
└ Back : プリミティブ 8 が無効です。 |
|
Engineer's Studio®の平板要素はアイソパラメトリック要素です。アイソパラメトリック要素では、正規化座標系で定義された形状関数よりモデル空間にある要素の座標を決めています。そのため、正規化座標系でのひずみをモデル空間の座標系でのひずみに変換する必要があります。ところが、この変換行列は直接求めることができません。そこで、モデル空間でのひずみを正規化座標系でのひずみに変換することが考えだされ、その変換行列をヤコビ行列と呼びます。必要なことは逆の変換なので、ヤコビ行列の逆行列が必要です。逆行列が存在するためにはヤコビ行列の行列式(ヤコビアンと呼ばれます)が正である必要があります。
図1のような形の四角形要素は、ヤコビアンが負になり、ヤコビ行列の逆行列が存在せず、計算を継続することができなくなります。そのため、Version 3.00.03まではソルバーエラーとなっていました。Version 3.01.00以降は、計算前チェックにおいて検出され、該当する平板要素名称とプリミティブ番号が情報として表示されます。
|
形が問題なくてもヤコビアンが負になる場合があります。図2は、三角形2次要素の例ですが、形は問題ありません。
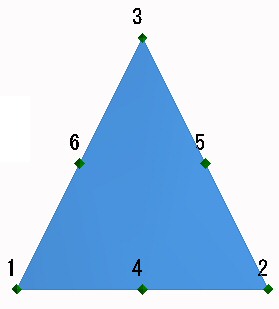 |
| ■図2 形状に問題がない三角形2次要素 |
計算できない原因は、要素の定義において、節点番号の並びが「4,2,5,3,6,1」になっていることです。節点4番は中間節点です。三角形二次要素では、中間節点から出発して定義するとヤコビアンが負になってしまいます。頂点である節点1番から出発するように「1,4,2,5,3,6」と定義すると、問題なく計算が可能になります。
平板要素を作成するコマンド(リボン「モデル|追加|平板」にある任意形状メッシュ要素、四角形メッシュ要素、アウトライン形状)を使って作成した場合はこのような問題は発生しませんが、手動でメッシュ要素のプリミティブを定義したときにみられます。プリミティブの節点名称の順番は、三角形や四角形の頂点からスタートして定義するように心掛けておくと安全です。 |
|
| (Up&Coming '14 新年号掲載) |
 |
|







>> 製品総合カタログ

>> プレミアム会員サービス
>> ファイナンシャルサポート
|








