�n��FEM��̓G���W�j�A�����O�̂��߂̓���u���̂U��ڂł��B
����́A��T�́u�ޗ��p�����[�^�̌��ߕ��v�ɂ��Đ������܂��B
���݁A���Ђ̒e�Y���n�Չ��GeoFEAS�ň����Ă���u�������`�e���v�A�u�e���S�Y���v�A�u�j��ڋߓx�@�v�ɂ��Đ������܂��B
���ʂɑ傫���e����^���邱�Ƃ���ޗ��p�����[�^�̌���͒n��FEM��͂ɂ����čł��d�v�ł���A�e�\�����ɕK�v�ȃp�����[�^��y����������K�ɔ��f���Ȃ���Ȃ�Ȃ��B�{�Z�~�i�[�ł́A��\�I�ȍޗ��p�����[�^�̐�����y�������l�Ƃ̊W�A��̓I�Ȍ�����@�ɂ��ĉ������B
�y�́A�}1�Ɏ����悤�ɔ��ɏ������Ђ��ݗ̈悩�����`���������B�������Ȃ���A�����̒n�Օό`���ł͒n�Ղɐ����Ă��鉞�̓��x���͒Ⴍ�A�K�Ȋ����ό`�W����p����A���`�e����͂ł��A�n�Ղ̕ό`�x�悭���߂邱�Ƃ��ł���B
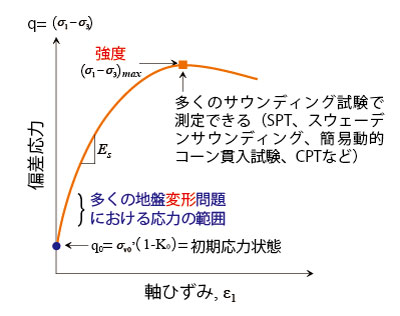
���}1�@�y�̔���`���́`�Ђ��݊W
�������`�e���ޗ��ɂ����āAE�͕ό`�W���Aν�̓|�A�\����AG�͂���f�W���ł���A�����̊ԂɎ��̊W������B
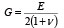 |
|
�i1�j |
���������āA�������`�e���ޗ��́A�ό`�W�� E �ƃ|�A�\���� ν ��2�̍ޗ��萔�����Ȃ��B����2�̍ޗ��萔�̒��ŁA�|�A�\����͔�r�I�e�ՂɌ��߂邱�Ƃ��ł���B�|�A�\����̌o���l�Ƃ��āA���̂悤�Ȓl���n��FEM��͂ł悭�p������B
- �S���y�F ν=0.35�`0.49
- �����y�F ν=0.25�`0.35
�y���ߌ@���g���l���@���͂ł́A�@��ɂ��d�͏������͂ɂ��Z�o�����B�������͂̐ݒ�ɂ�����A���d��͂ɂ���Đݒ肷��ꍇ�A���ʂЂ��ݖ��ɂ�����Î~�y���W���i�����W���Ƃ���ԁjK0�͒n�Ղ̃|�A�\���� ν �Ƃ̊ԂɎ��̂悤�ȊW������B
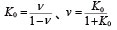 |
|
�i2�j |
�܂��A�`�p�̎{�݂̋Z�p��̊�A���z��b�\���v�w�j�ł́A�\1�Ɏ����悤�Ƀ|�A�\���� ν �Ɋւ���K�肪����B
| � |
�|�A�\����ν |
| �`�p�̎{�݂̋Z�p��̊ |
�O�a��r�������F ν=1/2���x�@���̑��̏����F ν=1/3�`1/2 |
| ���z��b�\���v�w�j |
�O�a�S���y�F ν=1/2���x�@���F ν=0.25�`0.35�A�ʏ��0.3
�֓����[���F ν=0.3�i�ʏ�j
�@�@�@�@�@�@�@�@ ν=0.15�i�Ԍ��䂪�傫���A���x���Ⴂ�ꍇ�j |
���\1�@��ɋK�肳�ꂽ�|�A�\����
�O�q�����悤�ɒn�Սޗ��͔���`��������A�ό`�W�����Ђ��݂Ɉˑ����Ă���B�\������ޕʂ̒n�Ղɐ�����T�^�I�Ȃ���f�Ђ��݃��x���A����ъe�펎���@�̂���f�Ђ��݂̑���͈͂�}2�Ɏ����B
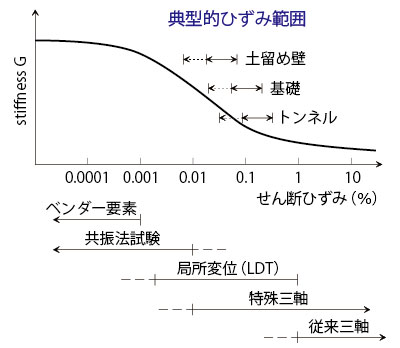
���}2 �ό`�W���̂Ђ��݃��x���̈ˑ����A�\�����ɂ��n�Փ��̓T�^�I��
�@�@ ����f�Ђ��ݔ͈́A�y�ъe�펎���@�̂���f�Ђ��݂̑���͈�
�ό`�W���̐�����@�Ƃ��āA��\�I�Ȃ��̂��ȉ��Ɏ����B
- ���ډ����ɂ����@�@
- �E�������ډ����ɂ����@
- �ꎲ�܂��͎O�����k�����ɂ����@
- �W���ѓ������ɂ��N�l����Z�o������@
- PS���w�ɂ�邹��f�g���x����Z�o������@
���̂悤�ȑ��֊W�ɂ��āA�g���̐��I�������n�߁A���҂��r������͑����BN�l�ƍE�������ډ������狁�߂��ό`�W�� Ep�̊W�́A�y���ɖ�킸Ep≈ 700N �����藧�B���ډ������狁�߂��n�Ղ̕ό`�W��Es�́AEp��3�`4�{�ƂȂ�B�܂��A�E�������ډ������瓾��ꂽEp�ƁA�O�����k������ꎲ���k�����Ȃǂ��瓾��ꂽE50�́A�n�Սޗ��ɌW��炸�قڈ�v���Ă���B���̂��߁A�u���H���������E����� IV�����\���ҁv�Ȃǂɂ�����n�Ք��͌W���̎Z��ɂ����ẮA�\2�Ɏ�����W��α��p��������s���Ă���B
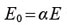 |
|
�i3�j |
�����ɁAE0�͒n�Օό`�W���Aα�͕\2�Ɏ�����Ă����W���AE �͕\2�̊e��@�ɂ��ό`�W���ł���B
| �ό`�W��E0�̐�����@ |
��W��α |
| �i�펞�j |
�n�k�� |
���a0.3m�̍����~�ɂ�镽�ډ����̌J�Ԃ��Ȑ����狁�߂��ό`�W����1/2
|
1 |
2 |
| �E�������ډ����ő��肵���ό`�W�� |
4 |
8 |
| �����̂̈ꎲ���k�������͎O���������狁�߂��ό`�W�� |
4 |
8 |
| �W���ѓ�������N�l���E0=2800N�Ő��肵���ό`�W�� |
1 |
2 |
| PS���w�̒e���g���x���Z�o�����ό`�W�� |
0.25 |
0.25 |
���\2�@�ό`�W���̐�����@
�܂��A���H���������ɂ́A�W���ѓ�������N�l���ό`�W���𐄒肷��Ƃ��A�n�Սޗ��̎�ނɂ�炸�ꗥ��2800�Ƃ����{����p���Ă��邪�A�g���l����͂ł́A�n�Ղ̕ό`�W���̐ݒ�ɑ��ẮA�E�������ډ������ʂ�p���邱�Ƃ������B��ʂɁA�W���ѓ������� N �l��� E=700N�ikN/m2�j�Ƃ��Đݒ肳���ό`�W���ƁA�E�������ډ����ɂ��ό`�W���́A�n�Սޗ��ɂ�炸�قڈ�v���Ă�����̂Ƃ���Ă���B���̂��߁A�y�،����������ɂ́AE=700N �Ƃ����o�������g���l����͂ɑE�߂��Ă���B
|
�@�e���S�Y�����f���̃p�����[�^�̌��ߕ� |
|
�e���S�Y�����f���ɂ́A�ό`�W���ƃ|�A�\����̂ق��A����f���x�萔�̔S����c�Ɠ������C�pφ�A�y�у_�C���C�^���V�[�p ψ ���K�v�ƂȂ�B
�n�Սޗ��̂���f���x�����߂鎎���͂���f�����ł���B��������f�����ɂ́A�ꎲ���k�����A��ʂ���f�����A�O������������B����f�����̌��ʂ́A�����̂̔r�������ɂ���Ē������ω����邽�߁A���������͌��n�ɂ�����O�͂̏����ƂƂ��ɔr���������Č����čs�����Ƃ��]�܂����B�������A���҂̑g�ݍ��킹�͌��n�ł͏ꏊ�I�E���ԓI�ɕω�����̂ŁA�Č��͓���B���̂��߁A�]�����玎�������͕\3�Ɏ����T�^�I��3��ނ̎��������ɏW��Ă���B
�\3����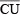 �����ł͈�����r���������ɊԌ������𑪒肵�A���ʂ�L�����͂ŕ\������B����ACD�����ł͊Ԍ����������݂��Ȃ����߁A�L�����͂͑S���͂ɓ������B���������āA�������̌��ʂ́A�L�����͕\���Ŕ�r���\�ł���B�����̒n�Սޗ��ɂ��āA�L�����͂ƂЂ��݂̊W��L���S�����Ɣj�͂̊W�́A�r�������ɉe������Ȃ��B���̏ꍇ�Ac’=cd�Aφ’=φd�ƂȂ�B �����ł͈�����r���������ɊԌ������𑪒肵�A���ʂ�L�����͂ŕ\������B����ACD�����ł͊Ԍ����������݂��Ȃ����߁A�L�����͂͑S���͂ɓ������B���������āA�������̌��ʂ́A�L�����͕\���Ŕ�r���\�ł���B�����̒n�Սޗ��ɂ��āA�L�����͂ƂЂ��݂̊W��L���S�����Ɣj�͂̊W�́A�r�������ɉe������Ȃ��B���̏ꍇ�Ac’=cd�Aφ’=φd�ƂȂ�B
| ���������̖��� |
�O�͍ډߒ� |
������
���x�萔 |
���n�̖͎����� |
�����ߒ�
|
����f�ߒ� |
����r���iUU�j����
|
��r�� |
��r�� |
cu�Aφu |
�S�y�n�Ղ̒Z��������i�}���{�H�j |
| ������r���iCU�j���� |
�r�� |
��r��
��̐� |
su/p |
���n�Ղ����������Ă���A�}���{�H |
������r��(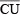 )���� )����
������̐ώ��� |
c’�Aφ’cu
ccu�Aφcu |
su/p |
�����r���iCD�j����
�����舳���� |
�r�� |
�r�� |
cd�Aφd |
���n�ՂȂǐZ�����̂悢�n�Ղ̎{�H�A
�n�Ղ̒��������� |
���\3�@�W���I�ȊO�͂̍ډߒ��Ɣr�������̑g�ݍ��킹
�}3�́A��s��������pc�A�̔S���y�ɂ�����3�̔r���������̂���f���x�̊T�O�}�ł���B�}3���́Aσb�͉߈����e�����́Aσa�̓_�C���C�^���V�[��0�ƂȂ鉞�͂ŁAσa�����ɊԌ������W���̕������ς��B
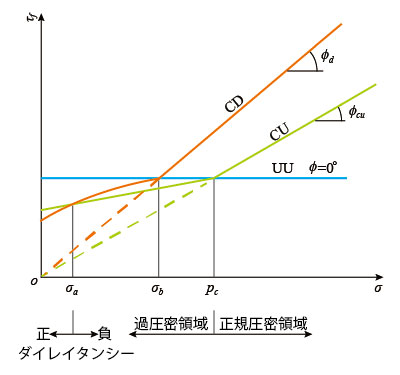
���}3 �r�������Ƃ���f���x�̊W
�}3�Ɏ�����Ă��鎎�����@�̎g�������͈ȉ��̂悤�ɐ����ł���B
- ���ȔS���y�n�Տ�ɋ}���ɐ��y�Ȃǂ̍ډׂ��s���ꍇ�A�ډג���ɔr�����قƂ�NjN���炸�A�������ܐ���̕ω��������Ȃ��B���Ȃ킿�A����r���iUU�j�����ɂȂ�B
- �n�Ղɑ���ډׂ����ɂ������ƍs���邩�A�n�Ղ̓��������傫���ډג��ɔr�������S�ɏI������ꍇ�A�ډׂƓ����ɒn�Ղ̔r�����s����̂ŁA�����r���iCD�j�����ɂȂ�B
- �v�����|�f�B���O�H�@�ȂǂŒn�Ղ���������������A�}���ɐ��y�Ȃǂ̍ډׂ��s���ꍇ�́A�j��ɑ��錟��������Ƃ��Ɏ��{����B
�܂��A�؎���@��Ȃǂɂ���Ă���f�ʂɍ�p���鐂�����͂�����������悤�ȉd����ꍇ�A�������͂̌����ɂ���Ēn�Ղ��z���c�����A���x���ቺ������Ԃ��댯�ƂȂ�B�}3�ɂ����āA��������σ�͈̔͂� σa<σ<pc �ł���Ζc����̔�r������f���x���Ⴂ�iCU�����j�̂ŁA���̂���f���x��p����Bσ<σa�͈̔͂ł͈����r���i�z���j�����̋��x�iCD�����j���z���̉e���ŏ������Ȃ�̂ŁA���̂���f���x���g�p����B
�����̋K���Ȃǂł́A�n�Ղ̍����ܗL���ɂ���č����y�ƔS���y�ɕ����āA�n�Ղ̔r�������������y�n�Ղ͊��S�r����ԁA�S���y�n�Ղ͊��S��r����Ԃł���Ƃ��Ă���B
�S���y�n�Ղł͕s���������̍̎�͔�r�I�e�Ղɍs���邪�A�����y�n�Ղł͕s���������̍̎�Ƃ����p�������������́A�S���y�n�Ղ̂���Ɣ�ׂāA�Z�p�I�ɂ���������A�R�X�g��������B���̂��߁A�����y�n�Ղ̋��x�萔�́A���ʒu�ɂ�����n�Ւ������ʂ��狁�߂邱�Ƃ������BTerzaghi & Peck�ȍ~�A���ʒu�ł̕W���ѓ������ő��肷�� N �l��苁�߂���@����������Ă���Ă���A�\4�Ɏ����悤�ɁA�e��v��Ɏ��グ���Ă���BN �l���獻�n�Ղ̓������C�p�����߂鎮�������ꂽ������g�p��̗��ӓ_�Ȃǂ͕������Q�Ƃ��ꂽ���B
�e���S�Y�����f���ŋ��߂����͂Ђ��݊W��}4�Ɏ����B�}4�Ɏ������悤�ɁA�_�C���C�^���V�[�p���������C�p�ɓ������ꍇ�A�Y����Ԃ̎��Ђ��݂ɑ���̐ςЂ��݂̔�� -2sinφ/(1-sinφ) �ł���Aφ=30°�̎��A-2sinφ/(1-sinφ)=-2 �ƂȂ�A�̐ϖc�����ߑ�ł���B��������邽�߂ɁA�_�C���C�^���V�[�p������K�v������A��ʂɎ��̂悤�ɐݒ肷��B
�@�S���y�n�ՁF ψ=0
�A���n�ՁFψ=φ’-�i20°�`30°�j�A�������Aψ �� 0
| �o�T |
φ(°)
|
qu(kN/m2) |
cu(kN/m2) |
�n�Ւ����̕��@�Ɖ��
(Terzaghi & Peck)
|
- |
12.5N |
- |
| Peck |
0.3N+27 |
|
|
| Dunham |
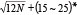 |
|
|
| ��� |
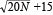 |
40+5N |
|
| ���݊�b�\���v�w�j�i2001�j |
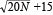 |
|
|
| ���H���������i1996�j |
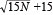 |
|
(6�`10)N |
| ���H���������i2002�j |
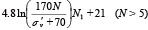 |
|
|
| �`�p�̎{�݂̋Z�p��̋K���i1999�j |
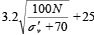 |
|
|
�S���\�������v�W���@
��b�\�����E�R�y���\�����i2000�j |
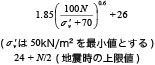 |
|
|
| ���z��b�\���v�w�j�i2001�j |
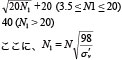 |
|
|
���\4�@N�l�Ɠ������C�p�A�ꎲ���k���x�A��r������f���x�̊W
| ��1�F |
*���x����l�Ŋۂ����qφ=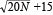 �A���x���z���悭�ۂ����E���x����l�Ŋp�������q �A���x���z���悭�ۂ����E���x����l�Ŋp�������q
φ=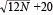 �A���x���z���悭�p�������qφ= �A���x���z���悭�p�������qφ=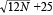 �B �B |
| ��2�F |
σν´�͗L����ڈ��ikN/m2�j�ł���B |
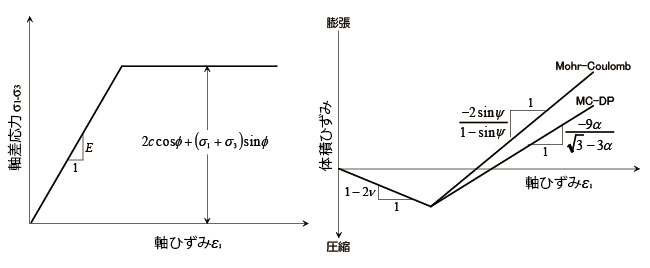
���}4 �e���S�Y�����f���̎��Ђ��݂Ǝ������͋y�ё̐ςЂ��݂̊W
|
�@�j��ڋߓx�@�̃p�����[�^�̌��ߕ� |
|
�ޗ��̔���`���l�������͂̏ꍇ�́A�e���╶�������ɂ����Ă�����`�e����͂���{�Ƃ��Ă��邱�Ƃ������B����`�e�����f���͒n�Ղ��Ղ̔���`��������萸�x�悭���ȕւɕ\�����Ƃ��\�ł���B�������A����`�e�����f���́A���`�e�����f���ɔ�ׂĕ��G�œ��̓p�����[�^�������A���̐ݒ�����Εs�����Ȍ��ʂ����ꂪ����B�g���l����͂ɂ͔j��ڋߓx�@���悭�p�����Ă���̂ŁA���̃p�����[�^�̐ݒ�ɂ��Đ�������B�j��ڋߓx�@�ɂ́A����f���x τR�A�������x σt�A�j�����`�w��a�A�ɂW��k�A����`�����W��m�An�Ȃǂ�����B
����f���xτR�A�������x σt�͎���������萄�肷��ق��A�����̒n�����d���̋����͂Ŏg�p���ꂽ���̂��Q�l���Č��߂邱�Ƃ��\�ł���B�j�����`�w��α�́A��ʓI�ɁA���̏ꍇ�́Aa = 1�i���̏ꍇ�A�j���̓��[���E�N���[���̔j���ƂȂ�j�A���̏ꍇ�́A1< a <2�A�d��̏ꍇ�́Aa = 2�ł���B
�ɂW��k�A�i�����{���H���c�ł͒e�����E�p�����[�^�ƌĂ��j�́A����`�e����̓��f���ɂ�����j��ڋߓx R �����߂邽�߂̃p�����[�^�ł���B�j��ڋߓx�@�ł́A�}5�Ɏ����悤�ɁA���`�̈�Ɣ���`�̈�Ƃ̋��E�ł� R’��R’e�Ƃ��A�ɂW��k=1/R’e�ƒ�`����ƁA���`�̈�Ɣ���`�̈�̋��E�ł́A�j��ڋߓx R ��1.0�ƂȂ�B�܂��A�}5.6�Ɏ�����Ă���悤�ɁA�j��ڋߓx R ��1.0�ȉ��̏ꍇ�ɂ͔���`�̈�ɂȂ�A1.0�ȏ�̏ꍇ�ɂ͐��`�̈�ɂȂ郂�f���ł���B�܂��A�j��ڋߓx R ��0.0�ȉ��̏ꍇ�ɂ́A�j��̈�ƂȂ�A�j���̕ό`�W���y�у|�A�\�����p���邱�ƂɂȂ�B
�j���̕ό`�W�� Df �Ƃ��ẮA��ʓI�ɍ�����������Ղɂ����Ă͏����ό`�W����1/100���x�A�������Ⴂ�n�Սޗ��ɂ����Ă�1/10���x���Ó��ł���ƍl�����Ă���B�j���̃|�A�\���� νf�́A��ʓI��0.45���x��p���邱�Ƃ������B
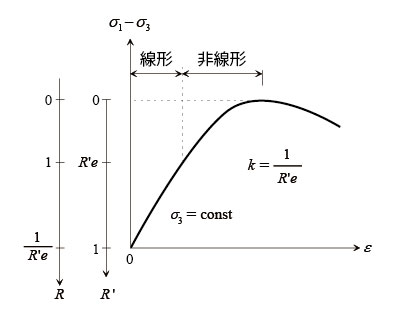
���}5 �O�������̉��́`�Ђ��݊W�A����єj��ڋߓxk
�\5�ɂ́A�����{���H���c�������Ă���ό`�W���ɑΉ������ɂW��k�ƁA��q�������`�����w�� m �̕W���l�������Ă���B�܂��A��Ղ̏����ό`�W���y�я����|�A�\����ɂ��ẮA�S�����݁E�^�A�{�ݐ����x���@�\��NATM�v�{�H�w�j�ł́A�n�R�v���ɉ����āAFEM��͎�@�̊�Ղɑ�����͕W���l�̖ڈ��Ƃ��ĕ\6�������Ă���B�����ɁA�\5�ƕ\6�̒l�͑����قȂ��Ă��邱�Ƃɗ��ӂ��ꂽ���B
�����ό`�W��D0
�iMN/m2�j |
�ɂW��
k |
����`�����w��
m |
| 10 �� D0 �� 100 |
2.0 |
1 |
| 100 �� D0 �� 1000 |
4.0 |
1/2 |
| 1000 �� D0 �� 10000 |
6.0 |
1/3 |
| 10000 �� D0 |
8.0 |
1/4 |
���\5�@�����ό`�W���ƊɂW���A����`�w��]
| �n�R���� |
�����ό`�W��D0
�iMN/m2�j |
����
�|�A�\���� |
�ɂW��
k |
����`�����w��
m |
���Ō�
�i�����y�j |
N�l10�`30 |
20 |
0.35 |
1 |
1/2 |
| N�l30�`50 |
50 |
| N�l50�ȏ� |
100 |
���E
���d�� |
IN |
50 |
0.30 |
10/3 |
1/4 |
| IIN |
100 |
| IIIN |
200 |
| ���d�� |
IVN |
500 |
0.30 |
10/3 |
1/4 |
| VN |
1000 |
| �d�� |
IIN |
2000 |
0.25 |
5 |
1/6 |
| IIIN |
5000 |
| IVN�ȏ� |
10000 |
���\6�@�n�R�����ɉ������W���l
����`�����w�� m �y�� n �́A�}6�Ɏ����悤�ɁA���ꂼ�����`�̈�̕ό`�W���y�у|�A�\����Ɣj��ڋߓxR�̊W���`������̂ł���B
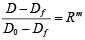 |
|
�i4�j |
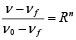 |
|
�i5�j |
�����ɁAD0�͏����ό`�W���Aν0 �͏����|�A�\����ł���B�܂��A�ʏ� n = m/2 �Ƃ���B����ɁA�����{���H���c�ł͔���`�����W����a�Ƃ��Ă���Aa��m �Ƃ̊Ԃ� m=1/a �̊W������B�S�����݁E�^�A�{�ݐ����x���@�\�ł͔���`�����w���� 1/n �Ƃ��Ă��邱�Ƃɗ��ӂ���K�v������B
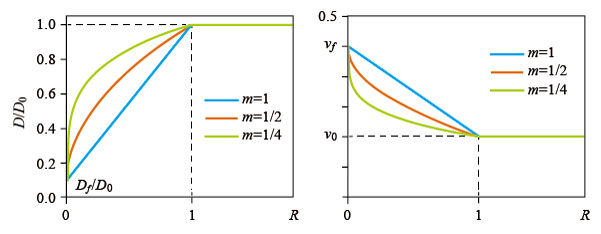
���}6 �j��ڋߓx�ƕό`�W���A�|�A�\����̊W
�t�H�[�����G�C�g�p�u���b�V���O�̏��ЃV���[�Y
�w�V�� �n��FEM ��͓���x�̂��ē�
�n��FEM��͂Ɋւ���L�x�Ȍo���ƌ������тɗ��t����ꂽ�n�Չ�͓��发�B
�n��FEM��͂̊�b���_�A���f�����O�Z�p�����A���l�ȉ�͎���ɂ��āAFEM��͂ɂ��������̃v���Z�X�ƌ��ʂ��킩��₷����������n�ՋZ�p�ҕK�g�̈��
���ďC�F�L�� �{�O�i�S���{�n���ׂ�w��,�Q�n��w�����j
�����ҁF�� ��i�Q�n��w�����j
��2013�N9��19�����s
��4�F�^245�y�[�W
��\3,800�i�ŕʁj
���t�H�[�����G�C�g �p�u���b�V���O��
�����Ђ̂��w���́A�t�H�[�����G�C�g�����T�C�g�܂���Amazon.co.jp�ŁI
|
 |
| �@���w�V�ŁE�n�� FEM��͓���x�ڎ��\�� |
| ��1�� |
�n�ՍH�w�ɂ�����FEM ���
�n��FEM��͂̕K�v���E�̌n�A��͎�ށA���l��͂̌덷 |
| ��2�� |
�n��FEM ��͂̊�b���_
�͊w�̊�b�A���ʂЂ��ݖ��Ǝ��Ώ̖��A�L���v�f�@�̊�b |
| ��3�� |
�n��FEM ��͂̂��߂̃��f�����O�Z�p
��͖ړI�A��@�A�����A�g���l���@���͂ɂ����鉞�͉���� |
| ��4�� |
�n�Սޗ��̍\����
���͕s�ϗʁA���`�e���\�����A����`�e���\���� �A�e���S�Y�����f���A�i�Y���\���� |
| ��5�� |
�ޗ��p�����[�^�̌��ߕ�
�������`�e���\�����A�e���S�Y�����f���A�j��ڋߓx�@�̃p�����[�^�̓�����@ |
| ��6�� |
�n�Ղƍ\�����̑��ݍ�p
�\�����̃��f�����A�C���^�[�t�F�C�X�̃��f���� |
| ��7�� |
����`���
�����@�ANewton-Raphson�@�A�J�Ԃ��v�Z�ɂ������������ |
| ��8�� |
����f���x�ጸ�@�ɂ�������
����f���x�ጸ�L���v�f�@�̏Љ�Ɖ��p�� |
| ��9�� |
�t�ɔ������d�ɂ��ό`���
��͎�@�A�p�����[�^�A��͎���A�_�\�����̐v�Ƃ̘A���@�\ |
| ��10�� |
��͎���
���y�̎Ζʈ���A �i�ǍY��b�̐��y�ډז��A�g���l���g���H���A���i�H�@�ɂ��n�Ղւ̉e����� |
| ��11�� |
GeoFEAS �̑�����@
�g���l���@��ɔ����ߐڍY��b�ւ̉e����́A����f���x�ጸ�@�ɂ��Ζʂ̈����� |
| ��12�� |
�n���M��͂ɂ���
�n���M�ɂ��āA�n���M��͂Ƃ� |
|








