|
�n��FEM��̓G���W�j�A�����O�̂��߂̓���u���̂V��ڂł��B����́A��U�́u�n�Ղƍ\�����̑��ݍ�p�v�ɂ��Đ������܂��B
���̑��ݍ�p�̖��������ꍇ�ɁA�n�ՁA�\�����A�y�сA���҂̋��E�ʂ����ꂼ�ꃂ�f��������K�v������B���f�����₻��ɕK�v�ȃC���^�[�t�F�[�X�ɂ��Đ������܂��B
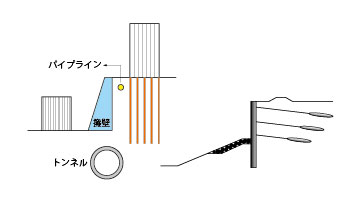
���}1�@�n�Ղƍ\�����Ƃ̑��ݍ�p
�����̒n�ՍH�w���ɂ͒n�Ղƍ\�����Ƃ����݂ɗ���ł���A�����̖���n��FEM��͂ʼn������Ƃ���Ƃ��A�n�ՁA�\�����A����ї��҂̋��E�ʂ����f��������K�v������B�}1�Ɏ����悤�ɁA�g���l����͂ɂ̓g���l���x�ۍH����ђn�ՁE�x�ۋ��E�ʂ��l�����邱�Ƃ��d�v�ł���B
�n�Ղƍ\�����Ƃ̑��ݍ�p���l������n��FEM��͂ɍ\�����i�Ⴆ�A�y���ߕǁA�ؗ��A�g���l���x�ۍH�A�A���J�[�A��b�Ȃǁj���܂ޕK�v������B���܂��͎O�����A���̗v�f�i�\���b�h�v�f�j��p���č\���������f�������邱�Ƃ́A���_�I�ɂ͉\�ł��邪�A���ۂɂ͕s���ȓ_������B��ʂɍ\�����̑傫�����S�̂̉�͗̈�ɔ�ׂĂ��Ȃ菬�������߁A���܂��͎O�����A���̗v�f��p���č\���������f��������ƁA�v�f�������ɑ����A�v�f�̌`�����Ȃ邱�Ƃ�����B
�܂��A�����̒n�Ս\�����̐v�ɕK�v�Ȃ̂́A�\�����̏ڍׂȉ��͏�Ԃł͂Ȃ��A�Ȃ����[�����g�A���́A����т���f�͂̒l�ł���B�\���������f����������܂��͎O�����A���̗v�f�̉��͂��Z�o�����A�\�����̋Ȃ����[�����g�Ȃǂ͋��߂��邪�A�lj��̌v�Z���K�v�ƂȂ��Ԃ�������B
���̂悤�ȕs���ȓ_��₤���߂ɁA�\�����̌`�邢�͕ό`�̗l�Ԃ���A���̓��������Ċȕւȃ��f�������{�����v�f�A���Ȃ킿�\���v�f��p���邱�Ƃ�����B���v�f��V�F���v�f�͂��̑�\�I�Ȃ��̂ŁA�O�����̍\���������ꂼ��ꎟ���A���ɑމ��������v�f�ł���B����܂łɑ����̍\���v�f����Ă���Ă���A���ꂼ�ꃁ���b�g�ƃf�����b�g������̂ŁA�\���v�f��p����ꍇ�A���̓����𗝉����A�������Ƃ�����ɓK�����\���v�f��I�ԕK�v������B�ȉ��ɗ��v�f�ɂ��ĊȒP�ɏЉ��B
�}2�ɗ��v�f�ɂ�����ߓ_�d�Ɛߓ_�ψʂ̕����K��i�������j�������B�����̕����K��͗����_�̒f�ʗ͂̕����K��Ƃ̊Ԃɑ��Ⴊ����B�f�ʗ͂̕����K��́A����ɂ��A���͈͂����𐳁A����f�͎͂��v���𐳁A�Ȃ����[�����g�͏㑤���k�ʼn��������ƂȂ�1�̋Ȃ����[�����g�𐳂Ƃ���B
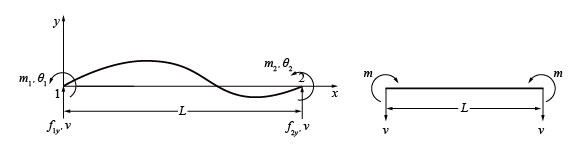
���}2�@���̕����K��i�������j ���F���v�f�̐ߓ_�d�Ɛߓ_�ψʁA�E�F�����_�̒f�ʗ�
�܂��A�������̉d���[���̏ꍇ���l����B���̒����ɔ�ׂĂ��̒f�ʂ̍��������Ⴂ�ɏ��������ɂ̓x���k�[�C�E�I�C���[�iBernoulli-Euler�j�̉��肠�邢�͕��ʁE���p�ێ��̉��肪���藧�B
���̎������̂Ђ��݂͎��̂悤�ɗ^������B
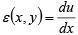 |
|
�i1�j |
�����ɁAu�͎������̕ψʊ��ł���B�}3�Ɏ����Ȃ��ɂ����̕ό`�l�Ԃ��A�������ix�����j�̕ψ�u��y�����̕ψ�v�Ƃ̊W��������B
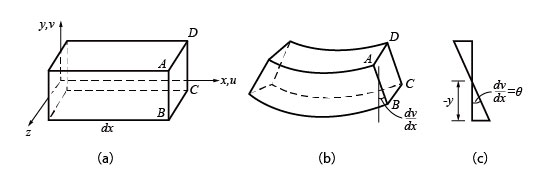
���}3�@���v�f�̕ό`�l�ԁia�F�ό`�O�Ab�F�ό`��A�f��ABCD�̉�]�p�j
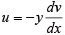 |
|
�i2�j |
���i1�j�Ǝ��i2�j���A������������B
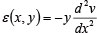 |
|
�i3�j |
�܂��A�����_���A�f�ʗ͂̋Ȃ����[�����g�Ƃ���f�͎͂��̂悤�� y �����̕ψ� v �ƊW�t���邱�Ƃ��ł���B
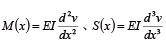 |
|
�i4�j |
���v�f��4�̎��R�x�����邽�߁A�v�f���� y �����̕ψʕ��z�����S3���������ŋߎ�����B
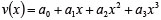 |
|
�i5�j |
3���������͗��̎x�z�����������A�����2�̗��v�f�����L����ߓ_�ł̕ψʂƉ�]�p�̘A�������ł���B
���v�f��2�̐ߓ_�ł� y �����̕ψʂƉ�]�p��p���āAa0�`a3 �����߂邱�Ƃ��ł���B
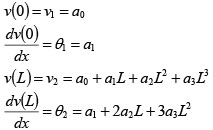 |
|
�i6�j |
�����ɁA��=dv/dx �͔����ȉ�]�p�ł���B���i6�j���Aa0�`a3 �����߁A���i5�j�ɑ������A�v�f���� y �����̕ψʊ������̂悤�ɕ\����B
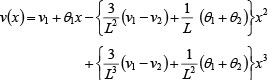 |
|
�i7�j |
����f�͂���ыȂ����[�����g�ɂ�������v�f�̐ߓ_�d�Ɨ����_�̒f�ʗ͂̕����K��𗯈ӂ��A���i7�j�Ǝ��i4�j���A������������B
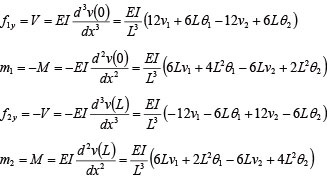 |
|
�i8�j |
���ɁA�������̌��ʂ�����B���̏ꍇ�A1�̐ߓ_��3�̎��R�x������B�������̉d�ƕψʂƂ̊W�͎��̂悤�ɗ^������B
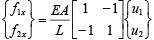 |
|
�i9�j |
�����ɁAA�͗��̒f�ʐςł���B
�������̌��ʂƂ���f�͋y�ыȂ����[�����g�̌��ʂ�g�ݍ��킹��A���̎�������x���Ƃ���Ǐ����W�ł̗͂ƕψʂƂ̊W�͎��̂悤�ɗ^������B
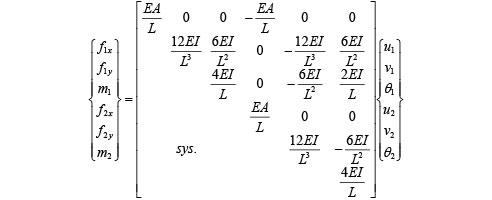 |
|
�i10�j |
�y���ߌ@��Ȃǂ�����ʂЂ��݉�͂ɓK�p����ꍇ�A�ؗ��Ȃǂ̉��s�������Ɉ��Ԋu�Ŕz�u�����\�����ɂ����ẮA���s�������P�ʒ����̋Ȃ�����EI�A�L�э���EA��p����悢�B
����ɁA�\�C���Z�����g����y���ߕǂ�g�|�Ɛ��t���R���N���[�g����Ȃ�NATM�g���l���̎x�ۍH�Ȃǂ͍������i���v�f�j�Ƃ��Čv�Z�ł���B�������@�̈����ȉ��Ɏ����
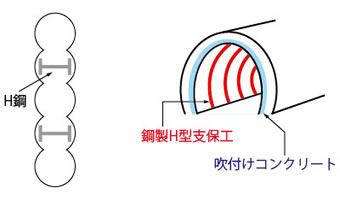
���}4 �������̗�i���F�\�C���Z�����g����y���ߕǁA �E�FNATM�g���l���x�ۍH�j
�܂��A�������̉d�ɂ��čl���悤�B�ȒP�̂��߁A��������2�̕��ނ���\�������Ƃ���B�������̎������̉d��P = εEA�A���އ@�ƇA�̎������̉d��P1 = ε1E1A1�AP2 = ε2E2A2�ŕ\����B���އ@�ƇA�̂Ђ��݂��������̂Ђ��݂Ɠ������iε = ε1 = ε2�j�A�������̎������̉dP = P1 + P2 �A�ʐ�A = A1 + A2�ł��邽�߁A�������̍���E�́A���̂悤�ɋ��߂���B
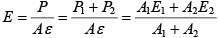 |
|
�i11�j |
���ɁA�Ȃ����[�����g�Ƌȗ� ρ �̊W���A�������̋Ȃ����[�����g��M = EIρ�A���އ@�ƇA�̋Ȃ����[�����g�� M1= E1I1ρ1�AM2 = E2I2ρ2 �ŕ\����B���އ@�ƇA�̂Ђ��݂��������̋ȗ��Ɠ������iρ=ρ1=ρ2 �j�A�������̋Ȃ����[�����gM = M1+ M2�ł��邽�߁A�������̒f�ʓ��[�����g�́A���̂悤�ɋ��߂���B
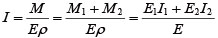 |
|
�i12�j |
�܂��A�v�y�ю{�H�ɍۂ��ċȂ��ϗ͂����҂��Ȃ����ނɂ����ẮA���̕��ނ̋Ȃ��������[���Ƃ��A���i12�j�ɑ�����������̒f�ʓ��[�����g�����߂�悢�B
|
�@�C���^�[�t�F�C�X�̃��f���� |
|
�n�Ղƍ\�����Ƃ̑��ݍ�p���ɂ́A�\�����ƒn�ՂƂ̊Ԃɑ��Εψʂ������邱�Ƃ�����B�A���̗v�f��p���ĉ�͂���ƁA�A���̗v�f�̓K�������A�v�f���E�ł��ׂ荇���v�f���m�̕ψʂ��A���ł��邽�߁A�}5(a)�Ɏ����悤�ɍ\�����ƒn�ՂƂ̋��E�Ő�����͂��̑��Εψʂ��Ȃ��Ȃ�B���̂��߁A�������̒n�Ղƍ\�����Ƃ̊Ԃ̕s�A���I���������f�����ł����@����Ă���Ă���B
- �����A���̗v�f��p����B���̗v�f�̍\�������A���̗v�f�̂��̂Ɠ����ł���B
- �n�Ղƍ\�����Ƃ̊ԂɃo�l�v�f�Ōq���B
- �������[���܂��͔����Ȍ�����������ȃC���^�[�t�F�C�X�v�f�i�W���C���g�v�f�Ƃ�����j��p����B
- �n�Ղ���э\�����͂��ꂼ�ꃂ�f�������A���̊Ԃɂ͓K������͂̂荇�������������������Ōq���B
���̒��ŁA�[�������̃C���^�[�t�F�C�X�v�f���ł��g���Ă���B�ȉ��ɃC���^�[�t�F�C�X�v�f�ɂ��ďЉ��B
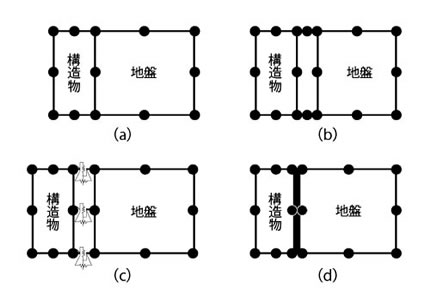
���}5 �n�Ղƍ\�����Ƃ̋��E�ʂ̃��f����
�ia�F�A���̗v�f�Ab�F�����A���̗v�f�Ac�F�o�l�Ad�F�C���^�[�t�F�C�X�v�f�j
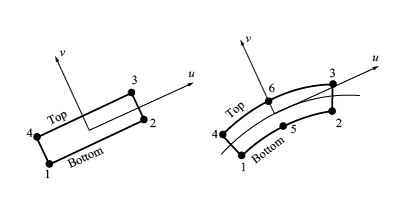
���}6 �A�C�\�p�����g���b�N�E�C���^�[�t�F�C�X�v�f
�t�H�[�����G�C�g�p�u���b�V���O�̏��ЃV���[�Y
�w�V�� �n��FEM ��͓���x�̂��ē�
����25�N9��19���AFORUM8�f�U�C���t�F�X�e�B�o��2013-3Days 2���ڂɁA�u�V�ŁE�n��FEM��͓���v�i�艿\3,800�i�ŕʁj�j���A�o�Ŕ�I���s���܂����B�{������ɂ������ẮA�Q�n��w ����A�L�������A�����āA�u���W�I�e�N�m �ԓc�l�ɐS��芴�Ӑ\���グ�܂��B�{���́A�n��FEM��͂̊�b���_�A���f�����O�Z�p�����A���l�ȉ�͎���ɂ��āAFEM��͂ɂ��������̃v���Z�X�ƌ��ʂ��킩��₷����������n�ՋZ�p�ҕK�g�̈���ƂȂ���̂ƍl���Ă���܂��B
���ďC�F�L�� �{�O�i�S���{�n���ׂ�w��,�Q�n��w�����j
�����ҁF�� ��i�Q�n��w�����j
��2013�N9��19�����s
��4�F�^245�y�[�W
��\3,800�i�ŕʁj
���t�H�[�����G�C�g �p�u���b�V���O��
�����Ђ̂��w���́A�t�H�[�����G�C�g�����T�C�g�܂���Amazon.co.jp�ŁI
|
 |
| �@���w�V�ŁE�n�� FEM��͓���x�ڎ��\�� |
| ��1�� |
�n�ՍH�w�ɂ�����FEM ���
�n��FEM��͂̕K�v���E�̌n�A��͎�ށA���l��͂̌덷 |
| ��2�� |
�n��FEM ��͂̊�b���_
�͊w�̊�b�A���ʂЂ��ݖ��Ǝ��Ώ̖��A�L���v�f�@�̊�b |
| ��3�� |
�n��FEM ��͂̂��߂̃��f�����O�Z�p
��͖ړI�A��@�A�����A�g���l���@���͂ɂ����鉞�͉���� |
| ��4�� |
�n�Սޗ��̍\����
���͕s�ϗʁA���`�e���\�����A����`�e���\���� �A�e���S�Y�����f���A�i�Y���\���� |
| ��5�� |
�ޗ��p�����[�^�̌��ߕ�
�������`�e���\�����A�e���S�Y�����f���A�j��ڋߓx�@�̃p�����[�^�̓�����@ |
| ��6�� |
�n�Ղƍ\�����̑��ݍ�p
�\�����̃��f�����A�C���^�[�t�F�C�X�̃��f���� |
| ��7�� |
����`���
�����@�ANewton-Raphson�@�A�J�Ԃ��v�Z�ɂ������������ |
| ��8�� |
����f���x�ጸ�@�ɂ�������
����f���x�ጸ�L���v�f�@�̏Љ�Ɖ��p�� |
| ��9�� |
�t�ɔ������d�ɂ��ό`���
��͎�@�A�p�����[�^�A��͎���A�_�\�����̐v�Ƃ̘A���@�\ |
| ��10�� |
��͎���
���y�̎Ζʈ���A �i�ǍY��b�̐��y�ډז��A�g���l���g���H���A���i�H�@�ɂ��n�Ղւ̉e����� |
| ��11�� |
GeoFEAS �̑�����@
�g���l���@��ɔ����ߐڍY��b�ւ̉e����́A����f���x�ጸ�@�ɂ��Ζʂ̈����� |
| ��12�� |
�n���M��͂ɂ���
�n���M�ɂ��āA�n���M��͂Ƃ� |
|








