残留変位照査は、H14/H24道路橋示方書V耐震設計編および下記文献1、2を参考にして実施されます。
- (財)海洋架橋・橋梁調査会、既設橋梁の耐震補強工法事例集、平成17年4月、p.II-97
- 前原康夫、鉄筋コンクリート橋脚の設計例とチェックポイント、 基礎工、総合土木研究所発行、2002.6
以下のような特徴があります。
- 橋脚天端節点の最大応答変位から基礎の回転による水平変位や基礎自身の水平変位を除去することによって、橋脚躯体自身の変形量δprを算出します(図1)。
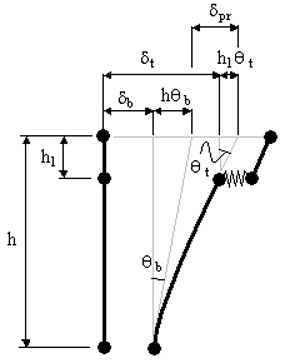 |
| ■図1 δprの概念図 |
δpr =δt +h1・θt −δb −h・θb
δpr :橋脚躯体の変形量
δt :橋脚天端の水平変位
δb :基礎底面の水平変位
※文献1では橋脚基部の変位、文献2では基礎底面の変位とされています。Engineer's Studio®ではフーチング底面と考えます。
θt :橋脚天端の回転角
θb :基礎底面の回転角
h :基礎底面から上部構造慣性力作用位置までの高さ
h1 :橋脚天端から上部構造慣性力作用位置までの高さ
- 各ステップで残留変位δRを逐次算出して、その中から最大値を求めます(図2)。
δR = cR・(μr−1)(1−r) δy
μr = δpr / δy
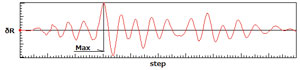 |
| ■図2 δRの時刻歴より最大値を算出 |
- 曲線橋や斜橋などの二軸曲げを受ける場合は、最大応答変位の方向での降伏変位をプログラムが自動的に算出します。
- 降伏変位δyは、H14/H24道路橋示方書V耐震設計編の地震時保有水平耐力を求める手法で自動算出します(※弊社製品『橋脚の設計』では厳密に算出されますがEngineer's Studio®では図3の曲率分布を積分する簡易手法です)。
 |
| ■図3 RC橋脚の曲率分布 |
|
図3のhは、フーチングの有無によって入力が異なります。
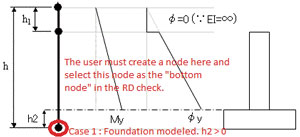
フーチング有りの場合
hには基礎底面からの高さを、h2にはフーチング厚を入力します(図4)。
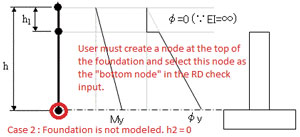
フーチング無しの場合
hには橋脚基部からの高さを、h2には0を入力します(図5)。
 |
 |
| ■図4 フーチング有りの場合 |
■図5 フーチング無しの場合 |
|
一例として、図6のような橋脚の入力例を示します。梁天端から上部構造慣性力作用位置までの高さは2.6mです。基礎ばねを考慮せず、フーチング底面を固定とし、タイプII地震動3波形を橋軸方向に与えた動的解析です。柱基部にM−φ要素、柱中間部は弾性梁要素です。
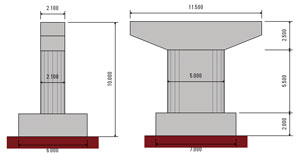 |
| ■図6 小判型橋脚(全高10m、底版厚2m) |
ケース1
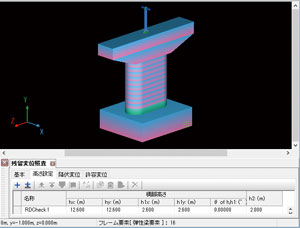
ケース1は、図7のようにフーチングと上部構造重心位置をモデル化した例です。上部構造分担重量に相当する質量598tが梁天端直上2.6mにあります。支承を表すばね要素の橋軸直角軸回りを自由とすることで梁天端にモーメントが作用しないようにしています。この場合、高さに関する入力は「h=12.6m、h1=2.6m、h2=2m」となります。降伏変位は梁天端直上2.6m位置で41mmです。
ケース2
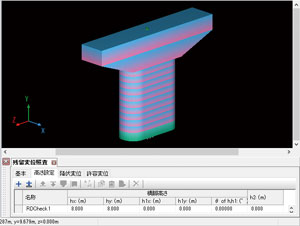
ケース2は、図8のようにフーチングと上部構造位置がないモデル化です。上部構造分担重量に相当する質量598tは梁天端位置に置いています。この場合、高さに関する入力は「h=8m、h1=0m、h2=0m」となります。降伏変位は梁天端で23mmです。
 |
 |
| ■図7 フーチング有り+上部構造重心位置有り |
■図8 フーチング無し+上部構造重心無し |
|
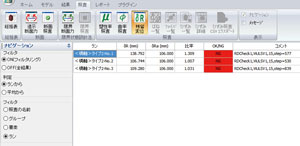
結果を図9と図10に示します。残留変位δRも許容値δRaもケース1の方がいずれも大きく、その差は約30%です。そのため許容値に対する比率はほぼ同じです(約3%の差)。
 |
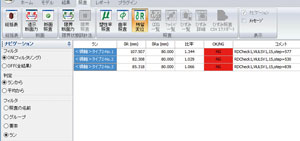 |
| ■図9 ケース1の結果 |
■図10 ケース2の結果 |
|
ケース1は全体系の中の1基を取り出したようなモデルです。ケース2は単柱RC橋脚の地震時保有水平耐力法の考え方を橋軸方向に関してモデル化した例です。モデル化方法によって、残留変位量と許容値に違いがでることがわかります。ただし、設計上の安全率はほぼ同じでした。ちなみに静的照査では残留変位は4.7mmでした。
弊社製品『橋脚の設計』からエクスポートした場合は、骨組みモデルがケース1で残留変位の入力はケース2というデータになり、残留変位照査結果はケース2とほぼ同じになります。
現状では正解と言えるモデル化方法は不明ですので、モデル作成と残留変位照査に関する入力について、本事例を参考にしていただき、実務設計にご利用いただけると幸いです。 |
|
| (Up&Coming '16 盛夏号掲載) |
 |
|







>> 製品総合カタログ

>> プレミアム会員サービス
>> ファイナンシャルサポート
|








