�^�����X�N��͂̕s�m�����ɂ���
|
�@ �^�����X�N�]���ɂ�����s�m���� |
|
�^�����X�N��͂ɂ�����s�m�����̓���
�����ł́A�^�����X�N��͂ɂ�����s�m�����̓����ɂ��ċ�̓I�ɐ�������B
�p�����[�^��f�[�^�̕s�m�������������߂ɁA�^�����X�N�̃}�N����͂̌v�Z�t���[�̊T�v��͎��I�ɐ}1�Ɏ������B�v�Z�̗���́A�~�J���x�Ȑ�����v��~�J�i�����W���^�n�C�G�g�O���t�j���쐬���A�����Z���×����f���iModel
1�j�ɓ��͂��ă��b�V�����ƂɐZ���[���v�Z����B�v�Z�����Z���[��Z����Q�Z�胂�f���iModel 2�j�ɓ��͂��A�Z���[�|��Q���Ȑ��Ǝ��Y�̕]���z�����Q�z���v�Z���A�����Ώۗ���S�̂ō��v���đ���Q�z���v�Z����B��Q�z�����Q�|�e���V�����Ȑ�������A�Č����Ԃ̊m�����x�Ȑ����悶�č^�����X�N�R�X�g���Z�o����B���ꂪ�v�Z�v���Z�X�̂����܂��ȗ���ł���B
|
|
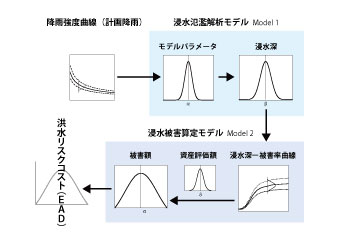 |
| �}1�@�^�����X�N�̃}�N����̓t���[�i�p�����[�^�̕s�m�������l���j |
|
�}1�ɂ͌v�Z�̗���ƂƂ��ɁA���f���v�Z�ɂ�����A���̓f�[�^�A���f���p�����[�^�A�o�̓f�[�^���m�����z�ŕ\�����Ă���A���̊m�����z�ɂ���Ă��ꂼ��̐��l�̕s�m������\�����Ă���B�����̐��l�̐ݒ�ɂ����āA�m���Ə��̎��W���s���A�m�����z�͂�蕝�̋������z�ƂȂ�A����ɂ���ĕs�m�����̒ቺ��\�����邱�Ƃ��ł���B����_�I���f���ł́A���̓f�[�^�����f���p�����[�^���o�̓f�[�^����̊m��I�Ȓl�Ƃ��ėp����B�������m���_�I�ȃ��f���ł́A���ׂĂ��m�����z���Ƃ��Ȃ������̂ƂȂ�A���̕��z���������s�m�������̕\���ƂȂ�B
�}1�ɂ����Ă܂��~�J���x�Ȑ����炠��Č����Ԃ��������v��n�C�G�g�O���t���쐬���邪�A�~�J���x�Ȑ����\���Ȋ��Ԃ̐����f�[�^�����Ƃɍ쐬����Ă���킯�ł͂Ȃ��B����܂ŗp���Ă��������s���lj͐암�̍~�J���x�Ȑ���35�N���̃f�[�^�����Ƃ�50�N�A100�N�m�����v�Z���Ă���A����ɋߔN�̑��J�X���̐V���ȍ~�J�f�[�^���lj������ƍ~�J���x�Ȑ����ω�����B�Z���×���̓��f���̐����v�Z�̃p�����[�^�ɂ����Ă��A�s�Z����̊����A�Z����̐Z���\�A�n�\�ʂ̓����e�x�ȂǓ��v�I�ȕ��ϒl��ݒ肷�邪�A������m�肵���l�ł͂Ȃ��A���ϒl�̂܂��Ɋm�����z��z�肹����Ȃ��B���ɁA�s�m��������������ɂ�����傫�Ȗ��Ƃ��ĉ�������Ă���̂��Z����Q�Z�胂�f���iModel 2�j�ł���B�f�[�^�̂�������܂�ɂ��傫���A����܂ł̌v�Z�ł͂��̂����F�߂Ȃ�����P�{�̐Z���[�|��Q���Ȑ��ő�\�����Ĕ�Q�z���v�Z�����B�������A���̂������e�Ղɐ��@�����悤�ɁA�v�Z���ꂽ��Q�z�A�����čŏI�I�ɓ�����^�����X�N�R�X�g�͂��Ȃ�̕s�m�������Ƃ��Ȃ������̂ɂȂ�ƍl������Ȃ��B�����v�Z���邾���Ȃ����ł悢���A���̍^�����X�N�R�X�g�����ƕ]���⎡����̈ӎv����ɂ����ėp����Ƃ��A�v�Z���ꂽ�l�͊m��l�ł͂Ȃ��A����m�����z���������������̂Ƃ��Ĉ������Ƃ����߂���B
|
�@ �^�����X�N�̕s�m�����̒�ʉ���@ |
|
�^�����X�N��͂ŗp����f�[�^��f���p�����[�^�͕s�m�������Ƃ��Ȃ��Ă���B���̕s�m�������ʉ�����ɂ́A�����̐��l���m�����z���������ϐ��Ƃ��Ă������B�m�����̍������l�قǁA���̕W�����͏������Ȃ�B����ł͂��̂悤�Ȋm�����z�Ƃ��ĕ\�����ꂽ���l��p���Ď��ۂ̌v�Z���s���ɂ͂ǂ�����悢���B
�悭�m���Ă�����@�̓����e�J�����V�~�����[�V�����ł���B
�����e�J�����V�~�����[�V����
�����e�J�����V�~�����[�V�����́A���܂��܂ȖړI�Ŏ��{����邪�A���̏ꍇ�A�m�����z�����������̓f�[�^���痐����p���Ė���ג��o�W�{�����A�������̓f�[�^�Ƃ��ă��f���ɓ��͂��A�v�Z�����o�͌��ʂɓ��̓f�[�^�̊m�����z�����f��������@�ƌ�����B���̓f�[�^�̊m�����z�̓f�[�^�̓����ɉ����ēK�ȕ��z��ݒ肷��B������Vose[1]�����Ƃɐ�������B
���܁A���̓f�[�^���}2���Ɏ������悤�Ȋm�����z�i�m�����x���jf(x)�������Ă���Ƃ���B���ꂩ��ݐϕ��z��F(x)�����߂�ƁA�m���ϐ�X��x�ȉ��ƂȂ�m���́A
F(x)=P(X��x)�@�@�@�@�@�@�@(1)
�ƂȂ�B������F(x)��0��1�̊Ԃ̒l���Ƃ�i�}2�E��j�B
����F(x)�̋t��G(F(x))�����߂�ƁAG(F(x))�͈ȉ��̎��ƂȂ�B
G(F(x))=x�@�@�@�@�@�@�@�@�@(2)
������F(x)��G(F(x))�̊W��}2���Ɏ����B������F(x)�́A0��1�̊Ԃ̒l���Ƃ�A�����ň�l���z(0�C1)���琶������闐��r��������B�}2���̉����ŗ���r�ɑΉ�����c���̕ϐ�x�����߂鑀����J��Ԃ����ƂŁA�m�����zF(x)�̖���ג��o�W�{�����������B
���̂悤�ɂ��ē��̓f�[�^�̖���ג��o�W�{����������A���̂ЂƂ̒l�����f���ɓ��͂��Čv�Z���s���B���̓f�[�^��2����ꍇ�́A�}3�̂悤�ɁA���ꂼ��̊m�����z���烉���_���ȃT���v���������A���������f���ɓ��͂��Čv�Z���ʂ����߂�B���̎��s�iRUN�j��N��i���ۂɂ͉�����ɂ��y�ԁj�J��Ԃ����Ƃɂ���ďo�͌��ʂ̕��z���������A���̓f�[�^�̊m�����z�f�������f���v�Z�̌��ʂ邱�Ƃ��ł���B���̃����e�J�����V�~�����[�V�����̌����͗e�Ղɗ����ł��邪�A�o�͌��ʂɂ����Ċm���炵���m�����z��̂ɉ����A������Ƃ������s���J��Ԃ��K�v������B
|
|
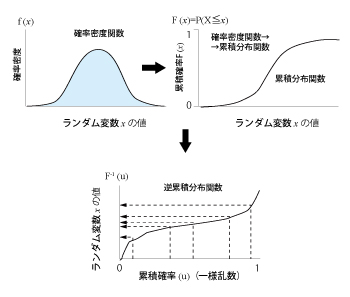 |
| �}2�@�����e�J�����@�ɂ��ϐ��̒��o |
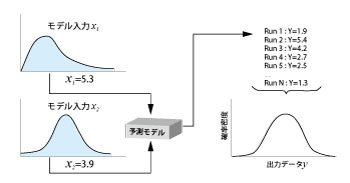 |
| �}3�@�����e�J�����V�~�����[�V�����̌v�Z�t���[ |
|
�^�����X�N�A�Z�X�����g�̌����ɂ����āA�����̕s�m�������͂ł́A���ʁA�~�J���x�Ȑ��A���X���A�Z���[�A��Q�z�A�C��ϓ��Ȃǂ��s�m�����̔������Ƃ���A�����̕s�m�����f�������X�N�A�Z�X�����g�����{����Ă���[2][3][4]�B�������A�������������̃I�[�_�[�ŌJ��Ԃ��v�Z���s��Ȃ���Ȃ炸�A���ꂪ�����e�J�����V�~�����[�V�����̑傫�ȕǂƂȂ��Ă���BVose[1]�́A���̂悤�ȍ����������@�Ƃ��āA����וW�{���o����菭�Ȃ����s�őg�D�I�ɍs�����e���n�C�p�[�L���[�u�@���Љ�Ă���B
|
�č����R�H�����̕s�m��������
�č����R�H�����̍^�����X�N��͂́A���X�N�A�Z�X�����g���^���Ƃ������R�ЊQ�ɓK�p�����ŏ��̎���ł���A���̌�̍^�����X�N��͂̔͗�ƂȂ������̂ł���[5]�B���X�N��͂̊�{�t���[���Ɋւ��Ă͐}4�ɂ��̌v�Z�t���[���������B�����ł�3�̋Ȑ���p���ČJ��Ԃ��v�Z���s���A�^���̒��ߊm���Ɣ�Q�z�̊W��\�����X�N�J�[�u���쐬���A���̋Ȑ���ϕ����ĔN�Ԕ�Q�z���ҒlEAD�iExpected
Annual Flood Damage�j���Z�o����B����EAD�͖{���ɂ�����^�����X�N�R�X�g�Ɠ����ł���B
�����A�}4�Ɏ����ꂽ�v�Z�̕��@�͌���_�I�ȃt���[���ł���A�s�m�������l�������v�Z�t���[�ł͂Ȃ��B���łɏq�ׂ��悤�ɁA���̗��R�H�����̍^�����X�N��͂́A�s�m�������͂��͂��߂č^�����X�N�̌v�Z�ɓK�p�������̂ł���A�����ŗp����ꂽ�����e�J�����V�~�����[�V�����́A���̌�̍^�����X�N�̕s�m�������͂̔͗�ƂȂ����̂ł���B����ł́A�}4�̌���_�I�t���[���ɂ����Ăǂ̂悤�Ƀ����e�J�����V�~�����[�V������K�p�����̂��낤���B
�}5����3�̐}�́A�ォ��A�^�����ʂƍ^���m���A�^�����ʂƍ^���ʁA�^���ʂƔ�Q�̊W��\���Ȑ��ł���B����_�I���@�ł͂����3�̋Ȑ��́A���ꂼ��m�肵���p�����[�^������1�{�̋Ȑ�����Ȃ�B�������A�����̋Ȑ������߂�p�����[�^���s�m�����������A�m�����z�����ϐ��ł���Ƃ���Ƃǂ��Ȃ邩�B�����Ő}5�Ɏ������悤�ɁA���ꂼ��̋Ȑ��̃p�����[�^�̊m�����z���痐����p���Ă��ꂼ��1�̃p�����[�^�̒l��ׂɎ��o���A3�̋Ȑ�������������irealization�j�B���̌�͏�q�̌���_�I�ȕ��@�ɂ���Ĕ�Q�z�Ɗm���̊W��\���Ȑ���1�{�쐬����B���̋Ȑ���ϕ�����ƁA����1��̎��s�ɂ��EAD�C���Ȃ킿�N�Ԕ�Q�z���Ғl���Z�o�����B���̂悤�ɗ�����p���ăT���v�����O���A�c��Ȑ���3�Ȑ��̑g���������A�����Ĕ�Q�z�|�m���Ȑ�����EAD���v�Z���鎎�s��������J��Ԃ����Ƃɂ��EAD�̊m�����z���ł�������B�������č^�����ʁA�^���ʁA��Q�z�̕s�m�����f�����N���ϔ�Q�z���ҒlEAD���v�Z�ł���̂ł���B
�č����R�H�����̍^�����X�N��͂ł͏�q�̂悤�Ƀ����e�J�����@�ɂ��EAD���Z�o����B�����Ő}5�̌v�Z�t���[�̓K�p��̂ЂƂ��ȒP�ɏЉ��B
�č��P���^�b�L�[�B�A���C�r���s�ɂ��闬��ʐ�158km2�̃x�A�O���X�E�N���[�N�iBeargrass Creek�j��ΏۂƂ�����͂ł���[5]�B�}5����3�̋Ȑ����ߋ��̃f�[�^�Ƀ��f���v�Z�����p���č쐬����B�����e�J�����V�~�����[�V�����Ŏ��s���J��Ԃ��A���s�̐�������EAD���Z�o����B���s���J��Ԃ��ɏ]���AEAD�̊m�����z���ł��������Ă����B���̌v�Z���ʂ����������̂̈ꕔ���\1�ł���B |
|
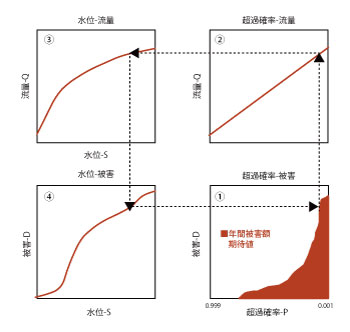 |
| �}4�@�ČR���R�H�����̍^�����X�N��͂̊�{�t���[�� |
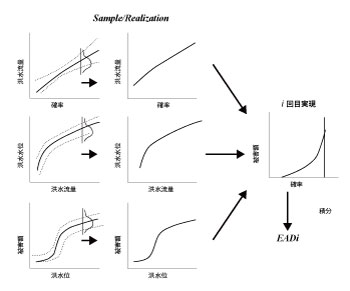 |
| �}5�@�����e�J�����V�~�����[�V�����ɂ��EAD�̌v�Z |
|
| �\1�@�s�m�������l�����Ȃ��ꍇ�ƍl������ꍇ�̔N���ϔ�Q�z���Ғl�iEAD�j�̌v�Z����([5]���j |
| Statistic |
EAD
without Plan |
EAD
with NED Plan |
Expected
Annual Benefits |
Annual
Project Cost |
Net Benefits |
Benefit to
Cost Ratio (B/C) |
Expected
no uncertainty |
3.015 |
0.937 |
2.078 |
0.81 |
1.268 |
2.56 |
Expected with
uncertainty (mean) |
3.998 |
1.684 |
2.314 |
0.81 |
1.504 |
2.86 |
| 25th Percentile |
* |
* |
1.365 |
0.81 |
0.555 |
1.69 |
| Median (50%) |
* |
* |
2.071 |
0.81 |
1.261 |
2.56 |
| 75th Percentile |
* |
* |
3.054 |
0.81 |
2.244 |
3.77 |
| (millions of US dollars per year) |
�\1�̍���̊D�F�ɓh��Ԃ��������́A�����v��NED(National Economic Development) Plan�����{���Ȃ��ꍇ�Ǝ��{�����ꍇ��EAD���A�s�m�������l�������ꍇ�ƍl�����Ȃ��ꍇ�ɂ��Ď��������̂ł���B�����v������{�����EAD�i���邢�͍^�����X�N�R�X�g�j�͒ቺ���邪�A�s�m�������l�����邩���Ȃ�����EAD�̌v�Z���ʂ��قȂ�B���{���Ȃ��ꍇ��EAD�͂��ꂼ��3.998, 3.015 million US$�^year�ƂȂ�A��҂���Ƃ���Ɩ�25���̈Ⴂ�ł���B�܂�����[5]�ɂ͎�����Ă��Ȃ����̂́A�\����*�Ŏ������Ƃ�������READ���v�Z����Ă���A2��ڂ���3��ڂ�������4��ڂ̐��l�iExpected Annual Benefits�j�͊m�����z�Ƃ��ĕ\������Ă���B���ϒlmean�̂ق��ɁA25th, 50th (median), 75th percentile�̐��l���番�z������m�邱�Ƃ��ł���B4��ڂ̒l�ŋC�������Ƃ́A�܂����ϒl�������l���傫�����Ƃ��番�z�͔�Ώ̂ł��邱�ƁA�����75-50th percentile�̒l�̍����A50-25th percentile�̂�����傫�����Ƃ���A���z�͐��̂Ђ��݂������Ă��邱�Ƃł���B
�ȏ�̂悤�ɁA�s�m�������l�����Čv�Z���s�����Ƃɂ��A���f���̃p�����[�^�̕s�m�����i�m�����z�j�f����EAD�����炽�Ȋm�����z�Ƃ��ĎZ�o����A���ϒl�̂܂��ɂ��镝�����������l�Ƃ���EAD�邱�Ƃ��ł���B���̃x�A�O���X�E�N���[�N�̗�ł́AEAD�ɕs�m�����͂�����̂́A������l�����Ă��\1�ʼnE���B�^C�͂��ׂ�1���Ă���ANED�����v��̌o�ϐ����m�F���邱�Ƃ��ł���B
|
�@ �^�����X�N�ɂ�����s�m������ʉ��̎��� |
|
�^�����X�N��͂ɂ����ĕs�m�������l������Ƃ��A�����e�J�����V�~�����[�V�����͏퓅�I�ȕ��@�ƂȂ�A2000�N��ɓ����đ����̕s�m�������͂������e�J�����@��p���Đi�߂��A�킪���ɂ����Ă��A�����[7]�́A�����e�J�����V�~�����[�V������p���āA���Q���v�Ȃǂ̊����f�[�^�����Ƃɓs�s��ɂ����鐅�Q���X�N�]����@�ɂ��Č������Ă���B�������A���łɏq�ׂ��悤�ɁA�����e�J�����@��K�p����ɂ͉�����ɂ��y�Ԍv�Z���v������邽�߃R���s���[�^�\�͂̐���Ƃ������ɓ˂�������B
�^�����X�N�ƕs�m��������
�^�����X�N�A�Z�X�����g�ɂ����Ċm���_�I���f��������Apel��[6]�́A�s�m�����̒�ʉ��ɂ��Č������A���X�N�A�Z�X�����g�̐M���������߂邽�߂ɂ́A�s�m���������v�Ȍ�������肵�A���̕s�m����������������ׂ��ł���Ƃ��Ă���[2]�B�����ĐZ����Q�\���ɂ�����s�m�����̒�ʉ��ɂ��Ă������̗L�v�Ȏw�E���s���Ă���B
- ���X�N�A�Z�X�����g�ɂ�����v�Z���ʂ́A����܂œ`���I�ɍs���Ă����v�Z�l�Ǝ����l�̔�r�����ł��Ȃ��ꍇ�������B�����ŕs�m�������͂�����ɂƂ��Ă������@�Ƃ݂Ȃ����Ƃ��ł���B
- ����܂ł̕s�m�������͂́A�n�U�[�h��́i�Ⴆ�Η��o��͂Ȃǁj�ɂ�������̂������A��Q�z�̌v�Z�Ɋւ�����̂͂���߂ď��Ȃ��B���ɁA�Z���[�Ɣ�Q���̊W�����f���ɂ���ĈقȂ�ƁA�����̐Z���[�̈Ⴂ����Q�z�̌��ς���ɑ傫�ȉe�����y�ڂ��B
- �Z���×��v�Z�ɂ����郂���e�J�����@�̓K�p�́A����܂�1�����͓��̒�h���o�ʂ���Z����̍L����ƐZ���[�����ς���ȑf�ȃ��f�����Ώۂł������B������2�����̐Z���×���̓��f���̌v�Z�Ƀ����e�J�����@��K�p���邱�Ƃ͂قƂ�Ǖs�\�ł���B�����v�Z�\�͂Ɩc��Ȍv�Z���Ԃ��v������邩��ł���B
- �����ׂ����ƂɁA2�����̐Z���[�̌v�Z�ɂ�����덷�͏����ȕs�m�������������Ȃ��B����͐Z���[�̌v�Z�ɑ����̌덷�������Ă��A���̃����_�����ɂ���Č덷�����ω�����A���ʂƂ��ĂقƂ�ǃ[���ɂȂ邱�Ƃ���������ł���B
�s�s�̍^�����X�N��͂ɂ�����s�m�������͂��l����ƁA�܂��Z���×����f���iModel 1�j�ɂ�����s�m����������B�킪���ł̐��I�Ȍ����Ƃ��āA���łɍ��R��[8]�̓����e�J�����V�~�����[�V������K�p���ė��o���f���̕s�m�����]�������݂Ă���B�����ΏۂƂ��郂�f����2�����×���̓��f���ł͂Ȃ��A�܂��^�����X�N��͂Ƃ����g�g�݂ł̌����ł͂Ȃ��B�s�s�̍^�����X�N��͂ɂ����ĕs�m���������d�v�ƂȂ�̂͐Z����Q�Z�胂�f���iModel
2�j�ɂ���Q�z�̎Z��ł���B
|
Model 1�ł̓��f���p�����[�^�̕s�m������Model 2�̂����菬�������ƁA�܂��O�҂̌v�Z���ʂ͎����l�₻��ɑ���f�[�^�ɂ���Ă�����x���؉\�ł��邪�A��҂̐Z����Q�Z�胂�f���ɂ����Ă͎����l�ɑ���������̂��Ȃ����ߌv�Z���ʂ̑Ó������������邱�Ƃ�����ł���Ƃ����������B���̂��߂ɂ��Z����Q�Z�胂�f���̌v�Z�ɂ����Ă͕s�m�������͂����d�v�ɂȂ�B
��Q�z�Z�胂�f���̕s�m����
�Z����Q�Z�胂�f���ł́A�Z���×���͂Ōv�Z�����Z���[����A�Z���[�|��Q���Ȑ��ɂ���Ĕ�Q�������߁A����ɕ����̕]���z���悶�ĐZ����Q�z���Z�o����B���̂Ƃ��Z���[�|��Q���Ȑ��������ł������Ɣ�Q�z���傫�ȉe������B�]���z�̐ݒ���s�m�������܂ނ��̂ł��邪�A�}6�ɂ��炽�߂Ď������悤�ɁA���̋Ȑ����쐬���邽�߂Ɏ��W���ꂽ�f�[�^�ɂ͂��Ȃ�̂��������B�����1�{�̋Ȑ��ő�\�����邱�Ƃ��ʏ�Ƃ�����@�ł��邪�A�����ŕ��ϓI��1�{�̋Ȑ��̎���ɕ��z���Ă���Ȑ��Q��z�肵�A�s�m�������͂����݂�B
|
|
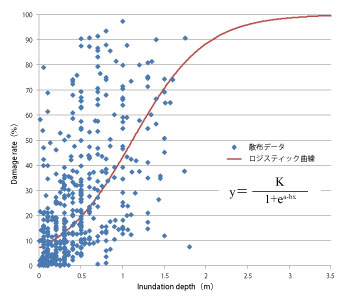 |
| �}6�@�Z���[�|��Q���Ȑ��i�ƒ�p�i�j |
|
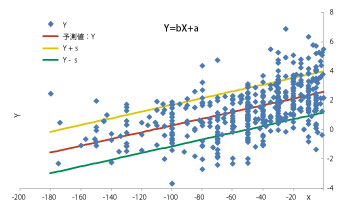
�Z����Q�Z�胂�f���ɂ�����Z���[�|��Q���Ȑ��̃��W�X�e�B�b�N�Ȑ��ւ̂��Ă͂߂ɂ��A�}6�̃f�[�^(x,y)���AX=-x�AY=ln((K-y)/y)�ɂ����(X,Y)�ɕϊ����ăv���b�g�������̂��}7�ł���B
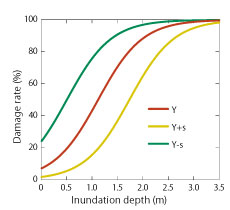
�����ɍŏ����@�Ō��肵���ꎟ��Y�ƕW�����̕������㉺�ɂ��炵��2�{�̐�Y+s�AY-s���������B�����3�{�̈ꎟ�����Ă�(x,y)�ɕϊ����ă��W�X�e�B�b�N�Ȑ��Ƃ��Ď��������̂��}8�ł���B�����ŕ��ϒlY����Y+s�AY-s�͈̔͂ɂ��āA�m�����z�𐳋K���z�ƌ��Ȃ��A�ق�70�������͈̔͂ɓ���ƍl���邱�Ƃ��ł���B
 |
 |
| �}7�@���W�X�e�B�b�N�Ȑ��쐬�̂��߂̈ꎟ���ϊ� |
�}8�@�Z���[�|��Q���Ȑ��i�ƒ�p�i�j
�@�@�@�i�W�����ɂ��s�m�������l���j |
�Q�l����
| [ 1 ] |
|
Vose, D: Risk Analysis - A Quantitative Guide,2nd edition, John Wiley &
Sons, 2000.
(�w���僊�X�N���́x�f���B�b�h�E���H�[�X�C�������[�C2003) |
| [ 2 ] |
|
Apel, H., Merz, B., and Thiken, A.H.: Quantification of uncertainty in
flood risk assessments, Intl. J. River Basin Management, Vol.6, No.2, pp.149-162,
2008. |
| [ 3 ] |
|
de Moel, H., and Aerts, J. C. J. H.: Effect of uncertainty in land use, damage models and inundation depth on flood damage estimates, Natural Hazards, Vol.58, pp.407-425,2011. |
| [ 4 ] |
|
de Moel, H.,Botzen, W. J. W., and Aerts, J. C. J. H.: Uncertainty in flood risk assessment: What are its major sources and implications?, Proceedings of the 2nd European Conference on Flood Risk Management Research into Practice (FLOODRISK 2012), Rotterdam, The Netherlands,19-23 November in 2012, 2013. |
| [ 5 ] |
|
National Research Council: Risk Analysis and Uncertainty in Flood Damage Reduction Studies, Washington, D.C., National Academy Press, 2000. pp.71-98. |
| [ 6 ] |
|
Apel, H., Thiken, A.H., Merz, B., and G. Bloschl: A probabilistic modelling system for assessing flood risks, Natural Hazards, Vol.38, pp.79-100. 2006. |
| [ 7 ] |
|
����~���C��y�_�i�F�����s�s���ɂ����鐅�Q���X�N�]����@�̊J���C�h�ЉȊw�Z�p�����������C��80 ���Cpp.1-6�C2012. |
| [ 8 ] |
|
���R�h�m�C������l�C���]�F���o���f���̕s�m�����]����@�Ƃ��̃��f���I���ւ̓K�p�C�y�؊w��_���W�CNo.789 �^�U -71�Cpp.1-13�C2005. |
�w�s�s�̍^�����X�N��� �`���Ђ��烊�X�N�}�l�W�����g�ց`�x
�^�����X�N�A�Z�X�����g�̍l�����ɂ��āA���̊�{�I�ȗ��_���@����A�}�N���E�~�N����͂ɂ�郊�X�N�]���ւ̉��p�A
�����I�ȓW�]�܂ł��킩��₷������B
| ������ |
�F |
��c �D�@(�ʼnY�H�Ƒ�w �H�w�� �y�؍H�w�� ����) |
|
�����i |
�F |
\2,800�i�ŕʁj |
| �����s |
�F |
2014�N11��25�� |
|
���o�Ŏ� |
�F |
�t�H�[�����G�C�g �p�u���b�V���O |
|
 |
�ڎ�
| ��1�́@ |
�^�����X�N���߂����āi���_�j |
��5�́@ |
�^�����X�N�A�Z�X�����g�Ƃ��̉��p�i�}�N���E�~�N����́j |
| ��2�� |
�s�s�ƍ^�����o |
��6�� |
�^�����X�N�̕s�m���� |
| ��3�� |
�^�����X�N�A�Z�X�����g�̊�{�t���[���@�@ |
��7�� |
�^�����X�N�̃A�Z�X�����g�ƃ}�l�W�����g�`�ۑ�Ə��� |
| ��4�� |
�^�����X�N�A�Z�X�����g�̎�@ |
|
|
�����Ђ̂��w���́A�t�H�[�����G�C�g�����T�C�g�܂���Amazon.co.jp�ŁI |
|








