|
�n��FEM��̓G���W�j�A�����O�̂��߂̓���u����8��ڂł��B����́A��7�́u����`��́v����A�y�̔���`�I�ȍޗ��������l���ł����͎�@�ɂ��ĉ�����܂��B
�n��FEM��͂ɂ��������`�ɂ͍ޗ�����`�Ɗw�I����`������B�w�I����`�͑�ό`��͂ƂȂ�B�ޗ�����`�͎�ɓy�̉��́|�Ђ��݊W�̔���`�ɂ����̂ł���B�y������`�ޗ��ł���ꍇ�ɂ́A�\���}�g���b�N�X�͈��łȂ��A���͂������͂Ђ��݂ƂƂ��ɕω�����B���������āA�y�̔���`�I�ȍޗ��������l���ł����͎�@���K�v�ƂȂ�B����܂ŁA�������̉�͎�@����Ă���Ă����B
����`��͂ł́A��ʓI�ɊO�͂ɂ�铙���ߓ_�̓x�N�g��F���������̑����ɕ�������B���Ȃ킿�A
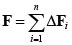 |
|
�i1�j |
�����ŁAn�͓����ߓ_�̓x�N�g���̑����̐��ł���B�܂��A���i2�j�����̂悤�ȑ����̌`�ɏ��������B
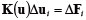 |
|
�i2�j |
�����ŁAK(u) �͑S�̐ߓ_�ψʃx�N�g���� u �ł���Ƃ��̑S�̍����}�g���b�N�X�AΔui �͑S�̐ߓ_�ψʃx�N�g���̑����i�ȍ~�A�ψʑ����Ɨ����j�AΔFi �͑S�̓����ߓ_�̓x�N�g���̑����i�ȍ~�A�d�����Ɨ����j�ł���B�e�X�̑S�̓����ߓ_�̓x�N�g���̑��� ΔFi �ɂ��ߓ_�ψʃx�N�g���̑��� Δui �����߂�A�g�[�^���̐ߓ_�ψʃx�N�g����������B
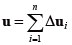 |
|
�i3�j |
�����@��p�������`��͂ł́A�}1�Ɏ����悤�ɁA�܂��A�d���� ΔF1 ����p�����A�S�̍����}�g���b�N�X K1 ���AΔF1 ����p����O�̏�Ԃł̉��͂�Ђ��ݓ���p���ĕ]�����������ŁA�������i2�j���ψʑ��� Δu1 ���v�Z����BΔF1 ����p����ߒ��œy�̍����͈��Ɖ��肵���̂ŁA�v�Z�œ���ꂽ�d�|�ψʊW�͐}1�Ɏ������� oa’ �ƂȂ�B�������A���� oa �̊Ԃł��ޗ������͈��łȂ��A�d�|�ψʊW�� oa �ł��邽�߁A�v�Z�덷 a’a ���o�Ă��܂��B�����@�ł́A���̌덷�����āA�v�Z��i�߂�B���ɉd���� ΔF2 ����p����B�S�̍����}�g���b�N�XK2���A�d���� ΔF1 ����p������Ԃł̉��͂�Ђ��ݓ��A���Ȃ킿�}7�Ɏ����_ a’�ł̉��͂�Ђ��ݓ���p���ĕ]�����������ŁA�ψʑ��� Δu2 ���v�Z����B�v�Z�œ���ꂽ�d�|�ψʊW�Ȑ��� a’ b’ �ł���A�ψʂ̌덷�� b’b �ƂȂ�B���̂悤�Ɋe�X�̉d�����ɂ��ψʑ������v�Z����B�v�Z�œ���ꂽ�d�|�ψʊW�́A�}1�Ɏ����悤�ɁA�Ȑ� oa’b’c’d’ �ƂȂ�A���ۂ̉d�|�ψʋȐ� oabcd �Ƙ������Ă���A�v�Z�ߒ��Ō덷���ݐς��Ă��邱�Ƃ��킩��B
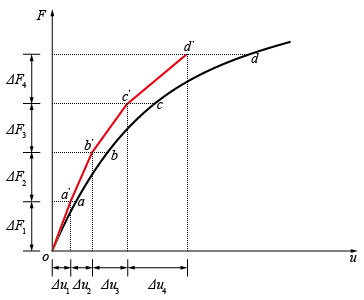 �� ���}1�@�����@
�����@�̐��x�͉d�����̃T�C�Y�Ɉˑ����邱�Ƃ����炩�ł���B�d�����̃T�C�Y����������A�d�����̐��������Ȃ�A��͎��Ԃ������Ȃ邪�A��͌��ʂ̐��x�������Ȃ�A���ۂ̉d�|�ψʋȐ��ɋ߂Â��Ă����B
�����@�ł͂���d�����ɂ��ψʑ������v�Z����Ƃ��A���Y�d��������p����O�̉��͂�Ђ��ݏ�Ԃ�p���āA�ڐ������}�g���b�N�X��]������̂ŁA���Y�d�����̊Ԃɐڐ������}�g���b�N�X���傫���ς��A�i���Ƃ��A�e����Ԃ��犮�S�Y����Ԃɕς��ꍇ��A�Y����Ԃ��珜�ׂŒe����Ԃɖ߂�ꍇ�j�A�v�Z�œ���ꂽ�ψʑ����̌덷�����Ȃ�傫���Ȃ邱�Ƃ����炩�ł���B�܂��A�����@�̌덷�͍ޗ��̔���`������������̓����Ȃǂɂ���ĈقȂ邽�߁A��͑O�Ɍ덷��\�����A�d�����̐������߂�͖̂w�Ǖs�\�ł���B
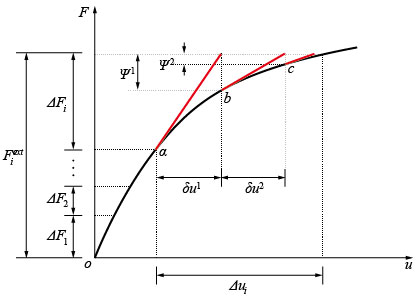
Newton-Raphson�@�ł́A�J�Ԃ��v�Z��p���āA�����@�Ŋe�X�̉d�����̉��Ő�����ψʑ����̌덷���Ȃ����Bi �Ԗڂ̉d�������Ƃ���Newton-Raphson�@�̌v�Z�菇���������B�܂��Ai-1�Ԗڂ̉d�����܂ł͌덷�������ł���قǏ��������̂Ƃ���Bi �Ԗڂ̉d��������p����Ƃ��̈��ڂ̌J�Ԃ��v�Z�͑����@�Ɠ����ł���B�v�Z�����J�Ԃ��ψʑ�����δu1�Ƃ���A���ڂ̌J�Ԃ��v�Z��̑S�ψʑ���Δui1=δu1�ł���B�����ŏ�Y�����͌J�Ԃ���\���B�}2�Ɏ����悤�ɁAΔui1�� Δui�̊ԂɌ덷�����݂���BΔui1��p���Ċe�v�f�̊e�K�E�X�_�ł̂Ђ��ݑ���Δεi1�͑����̌`�ŏ�������������莟�̂悤�ɓ�����B
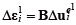 |
|
�i4�j |
 �� ���}2�@Newton-Raphson�@
����ɁA�e�v�f�̊e�K�E�X�_�ł̉��͑�������щ��͂����̂悤�ɓ�����B
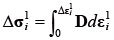 |
|
�i5�j |
| |
|
|
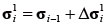 |
|
�i6�j |
�����ŁA�\���}�g���b�N�X D �͉��͂�Ђ��݂̊��ł���A�y�̉��́|�Ђ��݊W��p���Čv�Z����B���i5�j�Ŏ����v�Z�͉��͐ϕ��Ƃ������A���́|�Ђ��݊W�͔���`�ł��邽�߁A���x�����߂邽�߂ɁA�������̌v�Z��@�i�T�u�X�e�b�v�@��^�[���}�b�s���O�@�Ȃǁj����Ă���Ă����B�ł��ȒP�ȕ��@�͎��̂悤�ɉ��͑���Δσi1���v�Z����B
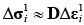 |
|
�i7�j |
���ɁA����Δσi1�Ɠ����Ȑߓ_�̓x�N�g���A���Ȃ킿���̓x�N�g�������i8�j���v�Z����B
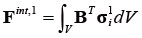 |
|
�i8�j |
ΔFi����p���Ă���Ƃ��̊O�̓x�N�g��Fiext�͎��̂悤�ɋ��߂���B
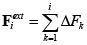 |
|
�i9�j |
�͂̂肠�����������߂ɁA���̓x�N�g���ƊO�̓x�N�g���͓������Ȃ���Ȃ�Ȃ��B�������A�}2�Ɏ����悤�ɁA���ڂ̌J�Ԃ��v�Z���I��鎞�_�ł́A���̓x�N�g���ƊO�̓x�N�g���̊Ԃɍ������݂��Ă���B���̍��͎c���̓x�N�g���Ƃ����A���̎��ŗ^������B
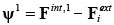 |
|
�i10�j |
���̎c���͂��Ȃ������߂ɁA���ڂ̌J�Ԃ��v�Z���s���B���̎c���̓x�N�g�����O�͂Ƃ��A���i2�j�������ƁA���ڂ̌J�Ԃ��ψʑ���δu2��������B
�����ŁAK(u) �͓_ b �ł̉��͂�Ђ��݂Ȃǂ�p���Čv�Z�����S�̍����}�g���b�N�X�ł���B���̌J�Ԃ��v�Z��̑S�ψʑ����͎��̂悤�ɋ��߂���B
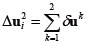 |
|
�i11�j |
���Ɉ��ڂ̌J��Ԃ��v�Z�Ɠ��l�ɁA���ڂ̌J�Ԃ��v�Z���I��������_�ł̂Ђ��ݑ���Δεi2�A���͑���Δσi2�A����σi2�A���̓x�N�g��Fint,2�A�c���̓x�N�g��ψ2�����ꂼ��v�Z����B
�ȏ�̂悤�ɁA�J�Ԃ��v�Z���i��ł����ƁA�}2�Ɏ����悤�ɁA�c���͂��i�X�������Ȃ�An��ڂ̌J�Ԃ��v�Z�œ���ꂽ�S�ψʑ���Δuin �͐����ɔ��ɋ߂Â����ƂɂȂ�B�c���͂� n ��ڂ̌J�Ԃ��v�Z�œ���ꂽ�ψʑ���δun �����ꂼ��̋��e�덷��菬������A�J�Ԃ��v�Z�����������Ƃ����A�J�Ԃ��v�Z���I������B���̎��_�Ōv�Z�����ψʁA�Ђ��݁A���͂Ȃǂ����̉d����ΔFi+1�̎n�_�Ƃ���B
Newton-Raphson�@�ɂ́A���̂悤��2�̎�_������B�@�e�J�Ԃ��X�e�b�v�őS�̍����}�g���b�N�X����蒼���āA���i11�j�Ɏ����悤�ɑS�̍����������������Ȃ���Ȃ�Ȃ����߁A��͂ɗv���鎞�Ԃ������Ȃ�B�A��֘A���ꑥ��L����e�Y���\�������g�p����ꍇ�ɂ́A�͂��߂͑Ώ̂ł������S�̍����}�g���b�N�X����Ώ̂ɂȂ�A���̂��߂̃\���o�[���K�v�ɂȂ�B
����2�̎�_���������邽�߂ɁA�C��Newton-Raphson�@�⏉�������@����Ă���Ă����B�C��Newton-Raphson�@�ł́A�}3�Ɏ����悤�ɁA�C�ӂ�1�̉d���� �ɂ����āA���ڂ̌J�Ԃ��v�Z�ŗp�����S�̍����}�g���b�N�X���A2��ڂ���̌J�Ԃ��v�Z�ł��g�p���邽�߁A�S�̍����}�g���b�N�X�̋t�}�g���b�N�X����߂�悢�B�����܂ł̌J�Ԃ��v�Z�̉������Ȃ邪�A�S�̂̌v�Z���Ԃ�Z�k���邱�Ƃ��ł���B�������A�C��Newton-Raphson�@�́A�Y����Ԃł̑S�̃}�g���b�N�X���v�Z���Ȃ���Ȃ�Ȃ����߁ANewton-Raphson�@�̎�_�A���������邱�Ƃ͂ł��Ȃ��B
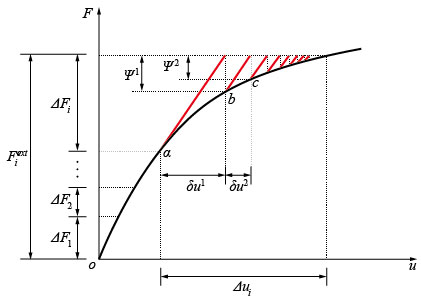 ��
���}3�@�C��Newton-Raphson�@
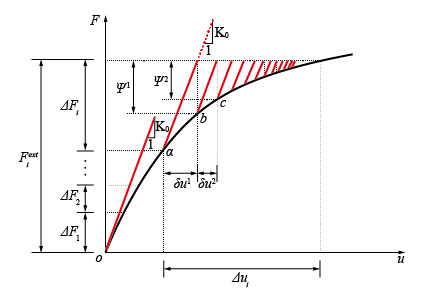 ��
���}4�@���������@
���������@�ł́A�}4�Ɏ����悤�ɁA�ŏ��̑S�̃}�g���b�N�X�A���Ȃ킿�d��������p����Ƃ��̈��ڂ̌J�Ԃ��v�Z�ŗp�����S�̍����}�g���b�N�X�����ׂẲd�����ɂ����邷�ׂĂ̌J�Ԃ��v�Z�Ŏg�p����B��ʂɉd����p����O�̏�Ԃł͑S�̌n���e����Ԃɂ���A�e���}�g���b�N�X��p���đS�̍����}�g���b�N�X�i���������}�g���b�N�X�j���쐬�ł��A�S�̍����}�g���b�N�X���Ώ̐��������߁ANewton-Raphson�@��C��Newton-Raphson�@������_�A���������邱�Ƃ��ł���B
����́A�u�y�̔���`�I�ȍޗ��������l���ł����͎�@�v�ɂ��ĉ�����܂����B�������Ȃ���A���ʂ̊W�ł��̑S�Ă��Љ�邱�Ƃ͂ł��܂��A��藝����[�߂����ꍇ�́A���ЂŊJ�Â��Ă���L���Z�~�i�[�Ȃǂ������p�肢�����Ǝv���܂��B����́u����f���x�ጸ�@�v�ɂ��ďЉ�v���܂��B�����҉������B
�t�H�[�����G�C�g�p�u���b�V���O�̏��ЃV���[�Y
�w�V�� �n��FEM ��͓���x�̂��ē�
�n��FEM��͂Ɋւ���L�x�Ȍo���ƌ������тɗ��t����ꂽ�n�Չ�͓��发�B�n��FEM��͂̊�b���_�A���f�����O�Z�p�����A���l�ȉ�͎���ɂ��āAFEM��͂ɂ��������̃v���Z�X�ƌ��ʂ��킩��₷����������n�ՋZ�p�ҕK�g�̈���ł��B
���ďC�F�L�� �{�O�i�S���{�n���ׂ�w��,�Q�n��w�����j
�����ҁF�� ��i�Q�n��w�����j
��2013�N9��19�����s
��4�F�^245�y�[�W
��\3,800�i�ŕʁj
���t�H�[�����G�C�g �p�u���b�V���O��
�����Ђ̂��w���́A�t�H�[�����G�C�g�����T�C�g�܂���Amazon.co.jp�ŁI
|
 |
| �@���w�V�ŁE�n�� FEM��͓���x�ڎ��\�� |
| ��1�� |
�n�ՍH�w�ɂ�����FEM ���
�n��FEM��͂̕K�v���E�̌n�A��͎�ށA���l��͂̌덷 |
| ��2�� |
�n��FEM ��͂̊�b���_
�͊w�̊�b�A���ʂЂ��ݖ��Ǝ��Ώ̖��A�L���v�f�@�̊�b |
| ��3�� |
�n��FEM ��͂̂��߂̃��f�����O�Z�p
��͖ړI�A��@�A�����A�g���l���@���͂ɂ����鉞�͉���� |
| ��4�� |
�n�Սޗ��̍\����
���͕s�ϗʁA���`�e���\�����A����`�e���\���� �A�e���S�Y�����f���A�i�Y���\���� |
| ��5�� |
�ޗ��p�����[�^�̌��ߕ�
�������`�e���\�����A�e���S�Y�����f���A�j��ڋߓx�@�̃p�����[�^�̓�����@ |
| ��6�� |
�n�Ղƍ\�����̑��ݍ�p
�\�����̃��f�����A�C���^�[�t�F�C�X�̃��f���� |
| ��7�� |
����`���
�����@�ANewton-Raphson�@�A�J�Ԃ��v�Z�ɂ������������ |
| ��8�� |
����f���x�ጸ�@�ɂ�������
����f���x�ጸ�L���v�f�@�̏Љ�Ɖ��p�� |
| ��9�� |
�t�ɔ������d�ɂ��ό`���
��͎�@�A�p�����[�^�A��͎���A�_�\�����̐v�Ƃ̘A���@�\ |
| ��10�� |
��͎���
���y�̎Ζʈ���A �i�ǍY��b�̐��y�ډז��A�g���l���g���H���A���i�H�@�ɂ��n�Ղւ̉e����� |
| ��11�� |
GeoFEAS �̑�����@
�g���l���@��ɔ����ߐڍY��b�ւ̉e����́A����f���x�ጸ�@�ɂ��Ζʂ̈����� |
| ��12�� |
�n���M��͂ɂ���
�n���M�ɂ��āA�n���M��͂Ƃ� |
|








