| �|�@UC-BRIDGE�����{�H��Ver.2.1x�̃g���u���ɂ��āi�ŏI�j�| |
�Q�O�O�O�N�T���R�O��
������Ѓt�H�[�����G�C�g
�T�|�[�g�����@����@forum8.co.jp |
| �P�D�͂��߂� |
| �@�{���i�̕����{�H�Ɋ֘A����v�Z���Ńg���u��������A�S���[�U�l�ɑ���Ȃ����f�����������Ă��܂��܂����B��ϐ\����܂���B�����ɁA���i�̏C���A���،��ʂɂ��đ����I�ɂ܂Ƃ߁A�ŏI���Ƃ��ĊF�l�ɂ��������܂��B |
| �Q�D�g���u���̓��e�Ƃ��̉e�� |
�@2�T�Ԓ��O�Ƀ��[�U�[�l����u����0���̎{�H�X�e�b�v�Ŏ包���d�ɂ��N���[�v�͂��o�Ă��邪�Ȃ����v�Ƃ̖⍇�킹���܂����B���̒l�̓R���N���[�g�̃����O�W���ϓ��̉e�����l���������̂Ǝv���܂������A���Ԃ�0���̊ԂɃN���[�v�͂������邱�Ƃ͎��Ԃƍ���Ȃ����ߒ������J�n���܂����B���̌��ʁA�N���[�v��͂ɂ�����u�N���[�v���̃����O�W����v�Ə̂��Ă��鏈�����s�\���ŁA�N���[�v�͂��ߑ�ɕ]������Ă��邱�Ƃ��������܂����B��̗���ȉ��Ɏ����܂��B
�@�@�ޗ�10���̕Ў�����̐�[�����d�ɂ��e���ό`��������Ƀs���Ŏx����ƃN���[�v�ɂ�肻�̎x�_�ɔ��͂������܂��B�{���i�̎Q�l�����Ƃ��ėp�����_��(1)�ł́A���̒l��R=32.1tf�i������j�ƂȂ��Ă���A���̃��f�������s���iVer.2.13�ʼn�͂����(��1�X�e�b�v�͕Ў�����A�����ɑ�Q�X�e�b�v�Ƃ��ăs���x�_��}��)�AR=34.73tf�Ɠ����܂��B
�@�@�Ƃ��낪�A�s���x�_��}��������A��3�X�e�b�v�ȍ~�ɃN���[�v���͂̐i�s�x�����邽�߂ɕ����̃_�~�[�X�e�b�v�i�{�H�������ς������̂ŁA�lj����ނȂ��A�x�_�̕ύX�Ȃ��j���l������ƁA���ʂ͉��\�̂悤�ɑ������Ă����܂����B |
�����s�łɂ��Ў������[�̎x�_���͂̌o���ω���
| ���ڍޗ� |
100 |
200 |
500 |
1000 |
2000 |
5000 |
9999 |
�� |
| �x�_���� |
-22.97 |
-37.38 |
-43.88 |
-51.80 |
-56.54 |
-60.51 |
-67.98 |
-75.34 |
|
���̌����́A�N���[�v��(�s�Ò��)����������̃X�e�b�v�i��L�ł͑�3�X�e�b�v�ȍ~�j�ŁA���̕s�Ò�͂ɂ��e���ό`�̍l�����s�\�����������Ƃɂ���܂����B
����̃g���u���͎{�H���@���u�����{�H�v�ɂ����Ƃ��ɁA�包���d�A�v���X�g���X�ɂ��FRAME��͌��ʂɉe����^���܂��B |
| �R�D�C���ł̌���(1)�@�|�_���Ƃ̔�r�| |
�@��L�̃g���u�����C�������ŁiVer.2.14�j�ōēx�A�Ў�����̉�͂��s�Ȃ������ʂ����\�ł��B
���̉�͂ł̓R���N���[�g�̃����O�W�������i�v����x���g�p�j�Ƃ��܂����B�Q��̃X�e�b�v���ōŏI���͂��v�Z�����R=32.255�ƂȂ�܂��B |
���C���łɂ��Ў������[�̎x�_���͂̌o���ω���
| ���ڍޗ� |
100 |
200 |
500 |
1000 |
2000 |
5000 |
9999 |
�� |
| �x�_���� |
-21.60 |
-25.08 |
-27.98 |
-29.43 |
-30.34 |
-31.53 |
-32.19 |
-32.263 |
|
| �ʂ̌��ؗ�Ƃ��āA�_��(2)�Ɍf�ڂ���Ă���v�Z����ȉ��Ɏ����܂��B���̌v�Z���3�a�ԘA�������{�H����14���T�C�N���ŏ�������o���ː݂�����̂ŁA���\�ł͎包�f�ʗ͂̍ŏI�l�i�e�����{�N���[�v���j��\�����Ă��܂��B�@ |
���R�a�ԘA�����̒��Ԏx�_��Ȃ����[�����g��
| ���_���̒l�� |
|
�� �C���łɂ��l�� |
| �@ |
�����x�_ |
�E���x�_ |
| �e���� |
-494 |
-702 |
| �N���[�v�� |
-318 |
-179 |
| ���v |
-812 |
-881 |
|
|
| �@ |
�����x�_ |
�E���x�_ |
| �e���� |
-494.0 |
-702.2 |
| �N���[�v�� |
-317.2 |
-182.5 |
| ���v |
-811.2 |
-884.7 |
|
|
| ���̂悤�ɁA�_���Ȃǂ̊J�����̎Q�l�����Ƃ̏ƍ��ł͏C���ł͗ǂ����x�Ōv�Z�ł��Ă��邱�Ƃ������Ă��܂��B |
�S�D�C���ł̌���
2)�@�|���v��Ƃ̔�r�| |
| �@���ɁA���v��i����2�N���{�j�Ɣ�r��������ȉ��Ɏ����܂��B���̌v�Z���5�a�ԘA�������{�H����40���T�C�N���Œ���o���ː݂�����ŁA���\�͍ŏI�̎包���d�ɂ��Ȃ����[�����g�������Ă��܂��B�i�@�j���̒l�͎��v��̒l��1.0�Ƃ����Ƃ��̔䗦�ł��B�@ |
| �@ |
���Ԏx�_�P |
���Ԏx�_�Q |
���Ԏx�_�R |
���Ԏx�_�S |
�P�[�X�@
���v�� |
�e���� |
-1740.6 |
-3360.4 |
-2883.0 |
-2900.6 |
| �N���[�v�� |
-1482.2 |
-872.5 |
-777.3 |
-1801.0 |
| ���@�v |
-3222.8 |
-4232.9 |
-3660.3 |
-4701.6 |
�P�[�X�A
Ver.2.14
Ec�F���
�ӁF���C�� |
�e���� |
-1750.8
( 1.0059) |
-3388.7
( 1.0084) |
-2906.5
( 1.0082) |
-2925.4
( 1.0085) |
| �N���[�v�� |
-1241.5
( 0.8376) |
-756.2
( 0.8667) |
-684.0
( 0.8800) |
-1530.0
( 0.8495) |
| ���@�v |
-2992.3
( 0.9284) |
-4144.9
( 0.9792) |
-3590.5
( 0.9809) |
-4455.4
( 0.9476) |
�P�[�X�B
Ver.2.14
Ec�F���
�ӁF�ύX |
�e���� |
�@-1750.8
( 1.0059) |
-3388.7
( 1.0084) |
-2906.5
( 1.0082) |
-2925.4
( 1.0085) |
| �N���[�v�� |
�@-1382.8
( 0.9329) |
�@ -887.9
( 1.0177) |
-777.4
( 1.0001) |
-1696.8
( 0.9421) |
| ���@�v |
-3133.6
( 0.9723) |
-4276.6
( 1.0103) |
-3683.9
( 1.0064) |
-4673.2
( 0.9940) |
�P�[�X�C
Ver.2.14
Ec�F���
�ӁF���� |
�e���� |
-1750.8
( 1.0059) |
-3388.7
( 1.0084) |
-2906.5
( 1.0082) |
-2925.4
( 1.0085) |
| �N���[�v�� |
-13991.9
( 0.9391) |
-862.3
( 0.9883) |
-762.2
( 0.9806) |
-1755.4
( 0.9747) |
| ���@�v |
-3142.7
( 0.9751) |
-4251.1
( 1.0043) |
-3668.7
( 1.0023) |
-4680.8
( 0.9956) |
�P�[�X�D
Ver.2.14
Ec�F��ޗ�
�ӁF���C�� |
�e���� |
-1788.9
( 1.0277) |
-3473.3
( 1.0336) |
-2974.5
( 1.0317) |
-2996.6
( 1.0331) |
| �N���[�v�� |
-1292.4
( 0.8719) |
-782.9
( 0.8973) |
-697.6
( 0.8975) |
-1623.2
( 0.9013) |
| ���@�v |
-3081.3
( 0.9561) |
-4256.2
( 1.0055) |
-3672.1
( 1.0032) |
-4619.9
( 0.9826) |
|
| �@�P�[�X�@�i���v��j�ƃP�[�X�A���ׂ�ƁA���̗�ł́A�N���[�v���̌��ʂ�15%���x�قȂ��Ă��܂��B���̈Ⴂ�͎g�p���Ă���N���[�v�W���i���\�j�̈Ⴂ�ɂ�镔��������܂����A���ꂾ���ł͂Ȃ��悤�ł����B |
| �@ |
��1step |
��2step |
��3step |
��4step |
��5step |
�ŏI |
| ���v�� |
0.82 |
1.06 |
1.22 |
1.36 |
1.54 |
2.54 |
| �P�[�X�A |
0.909 |
1.232 |
1.376 |
1.494 |
1.657 |
2.543 |
|
�@�����ŁA�����ɂ��Ĉȉ��̂悤�ɍl�@���܂����B
�������A�����_�ł͎��v��Ŏg�p���Ă���N���[�v��̓v���O�����̎d�l���T�v���x����������Ȃ����߁A���̎����Ɖ�͂ɗp�����Ă�����o�̓f�[�^���琄���ł���͈͓��ł̍l�@�ɂȂ��Ă��܂��B
�@�N���[�v��͂ōł��e���̑傫�����ڂ́A�N���[�v�W���Ƃ��̎g�����ł��B�{���i�̏ꍇ�́A���ڂ��Ă���a�Ԃɂ����āA���̕ό`�������鎞���i�R���N���[�g�ޗ߁j�ɑΉ������N���[�v�W�����v�Z���A�����e���ό`�ɏ悶�ăN���[�v�ψʂ��v�Z���Ă��܂��B
�@���Ƃ��A�A������1�a�Ԃ��Ƃɒ���o���ː݂���ꍇ�̑�1�a�Ԃɒ��ڂ���ƁA���̌a�Ԃ��{�H���ꂽ�Ƃ��̕ψʂɑ��ẮA���}��A�AB�AC�AD�̊e�_���N���[�v�W���ɂȂ�܂��B���ɑ�2�a�Ԃ��{�H���ꂽ�Ƃ��̑�1�a�Ԃ̕ψʂɑ��ẮAA'�AB'�AC'�̊e�_���N���[�v�W���ɂȂ�܂��B���̂悤�ɁA�ψʂ�������Ƃ��̃R���N���[�g�ޗ߂ɉ����āA�������ނɑ��ĈقȂ�Ȑ����g�p����܂��B |
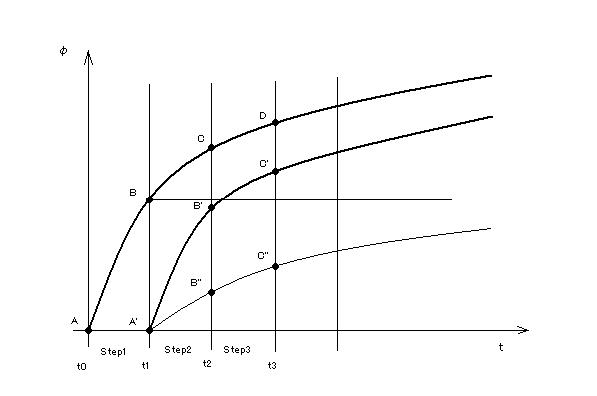 |
�@�Ƃ��낪�A���v��Ŏg�p���Ă���N���[�v��̓v���O�����̓��̓f�[�^�i�N���[�v�W���j�ł͊e�a�Ԃ��ƂɂP�̋Ȑ��������͂��Ȃ��i��}�ł�A-B-C-D�̋Ȑ��j�A�ޗ߂��i��ɐ�����ψʂ̂��߂̋Ȑ��i��}�ł�A'-B'-C'�̋Ȑ��j�͓��͂���Ă��܂���ł����B
�@�����ŁAA'-B'-C'�ɑ�����̂Ƃ��āAB-C-D�iA-B-C-D�Ȑ��̈ꕔ�j���g�p����Ă���̂łȂ����Ɛ������A������m���߂邽�߂ɖ{���i��p���Ď��Z���܂����B���ꂪ�P�[�X�B�ł��B
�@�P�[�X�B�̌��ʂ�����ƁA�N���[�v�W���̎g�p���@��ς��邾���Łi�l�͕ύX�Ȃ��j�A15%���x�̍���6%�O��܂ʼn��P����܂����B���̒l�͍ŏI�l�̂��̂ł����A�ːݓr���̑�2�X�e�b�v�I�����ɂ����钆�Ԏx�_��Ȃ����[�����g�́A�P�[�X�A�̏ꍇ-837.9tfm�i���v��ł�-1080.0�j�ł��������̂ɑ��A�P�[�X�B�ł�-1090.3tfm�ɕω����Ă��܂��B���̌��ʂ�����ƁA�ŏI���ʂɍ��͂�����̂́A�O�q�̐������Ó��Ȃ悤�Ɏv���܂��B
�@���ɁA�N���[�v�W�����̂����v��Ŏg�p����Ă���l�ɕύX�����Ⴊ�P�[�X�C�ł��B���̃P�[�X�ł́A��2�X�e�b�v�I�����̒��Ԏx�_��Ȃ����[�����g��-1028.7tfm�ł����B�ŏI���ʂ͑������P����Ă�����̂̈ˑR�Ƃ��č����c���Ă��܂��B���̍����Ȃ���������Ȃ����́A���v��Ŏg�p����Ă���v���O�����̏ڍd�l��������Ȃ����߁A�����ł��܂���ł����B
�@������A�̍l�@�Ǝ��Z�ɂ��A���v��Ŏg�p����Ă���N���[�v��̓v���O�����Ɩ{���i�ł̓N���[�v�W���̎�舵���ɈႢ�����肻���ł��B�O�o�̐}�ŋȐ�A-B"-C"�͋Ȑ�B-C-D�s�ړ����������̂ɂȂ��Ă���A���v���O�����̍ł��傫�ȈႢ�́A�_B'-B"�Ԃ̇��ӂ��l�����邩�i�{���i�j�ۂ��ɂ���Ǝv���܂��B���̕����͒��ڂ���a�ԈȊO���ː݂����Ƃ��ɁA���ڂ���a�Ԃɐ������ψʂɂ��x��e�����ɂقڑ������Ă���Ǝv���܂��B
�@�{���i�ł͂��̇��ӂ���ɍl�����Ă��܂����A���v��̃v���O�����ł̎�舵���̂悤�ɃN���[�v�W����ύX����@�\��lj����AVer.2.15�Ƃ��Ē������܂��B���̔ł�p����·��ӂ̉e���i�\�����f���A�{�H���@�ł��Ȃ�قȂ�j�����茳�ł��m���߂��܂��B
�@�Ō�̃P�[�X�D�́A�P�[�X�A�ŃR���N���[�g�̃����O�W���̎�舵�����u���v�ł͂Ȃ��A���ڎ��̃R���N���[�g�ޗ߂ɉ����Ď�ޗߎ��̃����O�W�����g�p������ł��B�d���ڂ�Ƃ��ɁA���̂Ƃ��̃����O�W�����g�p����FRAME��͂����Ă���̂ŏ����̒e���ψʂ��傫���A���̌��ʃN���[�v�ψʂ̌��ς�����傫���Ȃ��ăN���[�v�͂��傫�߂Ɍv�Z����܂��B�e�������ϓ�����̂́A�\������Ă��钆�Ԏx�_��̕��ނ�1�O�̃X�e�b�v�Ŏ{�H�ς݂̂��߃����O�W���i�����j���傫���Ȃ��Ă���A���̌��ʒf�ʗ͂����Ԏx�_��ɏW������X���ɂ���Ǝv���܂��B |
| �T�D���s��Ver.2.13�ƏC����Ver.2.14�̔�r |
| �@��L�܂ł̌��ŏC���ł͊T�ˑÓ��Ȍ��ʂ������邱�Ƃ�������܂����̂ŁA���Ɍ��s�łƂ̔�r���ȉ��Ɏ����܂��B���̕\�́A�O�o�̎��v��𗼃o�[�W�����Ōv�Z�������ʂł��B |
| �@ |
���Ԏx�_�P |
���Ԏx�_�Q |
���Ԏx�_�R |
���Ԏx�_�S |
�E���s��
Ver.2.13 |
�e���� |
-1637.8 |
-3339.4 |
-2834.8 |
-2793.0 |
| �N���[�v�� |
-1525.3 |
-1045.8 |
-977.4 |
-2052.7 |
| ���@�v |
-3163.1 |
-4385.2 |
-3812.2 |
-4845.7 |
�A�C����
Ver.2.14
Ec�F���
�ӁF���C�� |
�e���� |
-1750.8
( 1.0690) |
-3388.7
( 1.0148) |
-2906.5
( 1.0253) |
-2925.4
( 1.0474) |
| �N���[�v�� |
-1241.5
( 0.8139) |
-756.2
( 0.7231) |
-684.0
( 0.6998) |
-1530.0
( 0.7454) |
| ���@�v |
-2992.3
( 0.9460) |
-4144.9
( 0.9452) |
-3590.5
( 0.9418) |
-4455.4
( 0.9195) |
�D�C����
Ver.2.14
Ec�F��ޗ�
�ӁF���C�� |
�e���� |
-1788.9
( 1.0923) |
-3473.3
( 1.0401) |
-2974.5
( 1.0493) |
-2996.6
( 1.0729) |
| �N���[�v�� |
-1292.4
( 0.8473) |
-782.9
( 0.7486) |
-697.6
( 0.7137) |
-1623.2
( 0.7908) |
| ���@�v |
-3081.3
( 0.9741) |
-4256.2
( 0.9706) |
-3672.1
( 0.9632) |
-4619.9
( 0.9534) |
|
�\���́i�@�j���̒l��Ver.2.13�̒l��1.0�Ƃ����ꍇ�̔䗦�������Ă��܂��B�܂��AVer.2.13�̌��ʂ͍ډ��ޗ߂�11���ɕς��čČv�Z�������̂ŁA�O��̕i����͍ޗ߂S���̏ꍇ�j�Ƃ͌��ʂ��قȂ��Ă��܂��B
�@���v�l�̍��́A���̔�r�ł́A���Ԏx�_�S�ōő�8%���x�������Ă��܂��B
�@���ɁA�ߋ��̃��[�U�l�̎���ɓY�t����Ă����v�f�[�^�i15�P�[�X�j�ɂ��āA���s�łƏC���ł̔�r���ȉ��Ɏ����܂��B���̕\�́A���s�ł̎包���d�̍ŏI�l�i�e�����{�N���[�v���j����ɂ������\�������̂ŁA���Ԏx�_��̋Ȃ����[�����g�ɂ��Ĕ�r���Ă��܂��B |
| �@ |
���f�� |
�d���F��� |
�d���F��ޗ� |
| 1 |
�S�a�ԘA���� |
1.0133 |
1.0131 |
| 2 |
�S�a�ԃ��[������ |
0.9557 |
0.9895 |
| 3 |
�T�a�ԃ��[������ |
0.9366 |
0.9755 |
| 4 |
�S�a�ԘA���� |
1.0137 |
1.0136 |
| 5 |
�S�a�ԘA���� |
1.0140 |
1.0137 |
| 6 |
�S�a�ԘA���� |
1.0062 |
1.0062 |
| 7 |
�T�a�ԘA���� |
1.0154 |
1.0155 |
| 8 |
�T�a�ԃ��[������ |
0.9837 |
0.9926 |
| 9 |
�V�a�ԘA���� |
0.9794 |
1.1004 |
| 10 |
�W�a�ԘA���� |
0.9263 |
1.0380 |
| 11 |
�S�a�ԘA���� |
1.0474 |
1.0031 |
| 12 |
�S�a�ԘA���� |
0.9997 |
0.9999 |
| 13 |
�T�a�ԃ��[������ |
0.9838 |
0.9830 |
| 14 |
�Q�a�ԃ��[������ |
0.9997 |
0.9997 |
| 15 |
�R�a�ԃ��[������ |
1.0084 |
1.0082 |
|
�@�\�����f���A�{�H���@�Ȃǂɂ��قȂ�܂����A���ɂ�10%�i�P�[�X9�j�̍��������Ă���P�[�X������܂��B���������āA���Ɍ��s�ŁiVer.2.13�ȑO�̔Łj�ŕ����{�H�̌���������Ă���ꍇ�́AVer.2.15�iVer.2.14�ɃN���[�v�W���̎g�p���@��ύX�ł���悤�ɂ����ŁF�O�o�j�ōČv�Z���Ă��������܂��悤���肢�������܂��B
�@�Ȃ��A�O�o�̎��v��Ȃǂ̂悤�ɉߋ��̎��т̑������R���N���[�g�̃����O�W�������Ƃ��Čv�Z���Ă���悤�ł��B���̂��߁A�{���i�ł����̂悤�Ȏ�舵�����\�Ȃ悤�ɋ@�\��lj����Ă��܂��iVer.2.14����j�B�{���i�̎g�p�ړI���ߋ��̎���Ƃ̔�r�Ȃǂɂ���ꍇ�A�����{�H��{�f�[�^�Ɋ܂܂�Ă���t���O�u��ޗߎ���Ec�̐���v�́u�v��l�i���͒l�j�v�����I�т��������B |
| �U�D������ |
�@����̃N���[�v��͂ɔ����g���u���ł̓��[�U�l�ɑ���Ȃ����f�����������A���ɐ\����܂���ł����B��N12���ɕ����{�H�ł������[�X����ۂɎQ�l�����̗��Ƃ͌��ʂ��ƍ����Ă������̂́A��蔭�W�����������s�\���ł���A�ߋ��̎��v��Ƃ̔�r���s�Ȃ��Ă��܂���ł����B
�@�܂��A�����{�H�łɂȂ��Ă���g�p���@������Ȃ������߂ɑ����̃��[�U�l����v�����Ăق����|�̂��v�]���Ă��Ȃ���A����ɑΉ����Ȃ��܂܍����Ɏ����Ă��܂����B
�@���������[�X�̎��_�Ŗ{�̂悤�Ȏ��v��Ɣ�r�����g�p�����Ă������̂悤�Ȃ��Ƃ͔�����ꂽ�Ǝv���܂��B
�@����́A�P�Ƀe�X�g���J��Ԃ��݂̂ł͂Ȃ��A�ߋ��̎��т��鐻�i�Ƃ̔�r��i�̌����s���A���[�U�l�ɂ��ׂĂ̏����I�[�v���ɂ��Ă������ƂŁA���i�̐M���������߂����ƍl���܂��B |
| �ȏ�A�������܂��B |
| ���Q�l������ |
����̕��쐬�ŎQ�l�ɂ����������ȉ��Ɏ����܂��B�������A���v��������܂��B
(1)�����A�n�ӂق��F�ψʖ@�ɂ��R���N���[�g�\�����̃N���[�v�E�������k��͂̊�b���_�A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�v���X�g���X�g�R���N���[�g�AVol.22�No.2�Apr.
1980
(2)�R�ƁA�n�ӁF�����{�H�����PC�A�������̒x��e�����l�������N���[�v��́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�v���X�g���X�g�R���N���[�g�AVol.21�No.5�Oct.
1979 |
| �����f�[�^�� |
����̕��쐬�Ŏg�p�����f�[�^�i���\�j��Ver.2.15�ɕt�����Ă��܂��BVer.2.15�ȍ~�̔łł����p���������B
| �t�@�C���� |
���@�@�@�@�@�@�@�� |
| Kensyou_02 |
�Q�l����(1)�̌v�Z�� |
| Kensyou_03 |
�Q�l����(2)�̌v�Z�� |
| Mykensyou_08 |
���v��Ƃ̔�r�̂����A�P�[�X�A�i�B�A�D�͂�����C���j |
| Mykensyou_08z |
���v��Ƃ̔�r�̂����A�P�[�X�C |
|








