WebLesson:#5
柱部材の変形特性:繰返し挙動
-強震時の変形挙動- |
はじめに
部材の変形挙動は荷重-変位関係の包絡線(P-??曲線)が基本となるが,地震時には,大小の地震波により,複雑な繰返し挙動を呈する.ここでは,実験と解析(シミュレーション)の両面から,繰返し挙動の勘所を考察したい.
本報では,まず,柱部材の交番載荷実験から繰返し挙動を観察し,1サイクルの特徴とパターンを説明する.また,動的解析に用いる履歴モデルを紹介し,これらを用いた数値シミュレーションを2例提示する. |
1. 実験結果から見た繰返し挙動:曲げせん断耐力比の異なる2試験体の挙動
耐震性に関する静的載荷実験は,通例,変位制御による正負交番載荷を行い,崩壊に至るまでの繰返し挙動から,耐荷力,変形性能,エネルギー吸収能力,破壊形式を観察するものである.地震時の挙動を把握するには,繰返し載荷時における部材の応答性状を仔細に観察し,理解することから始まる.
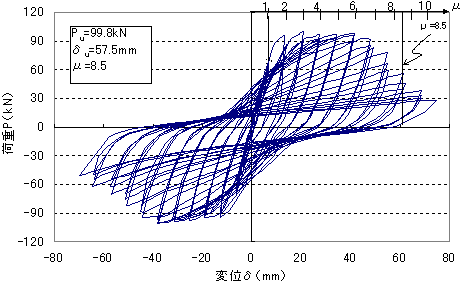
そこで,2体のモデル試験体による静的載荷実験の実験結果を紹介する(図1).この実験は,下端固定/上端載荷による片持ち梁形式(高さ(スパン)=1.2m)による交番載荷実験であり,橋脚(柱部材)を対象にした最も典型的な静的耐震実験である.本実験では,寸法形状および軸方向筋量(主鉄筋比)を含む断面諸元を同一とし,横補強筋(せん断補強筋の間隔と鉄筋径)をパラメータとして,実験したものである
| (1)S20試験体(曲げせん断耐力比2.51,曲げ破壊) |
 |
|
 |
(2)S10試験体(曲げせん断耐力比1.08,曲げ破壊) |
 |
|
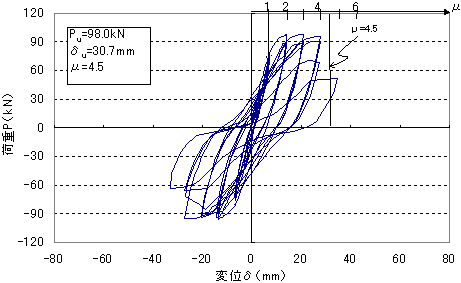 |
図1 正負交番変位制御型繰返し載荷実験の実験結果
(構造寸法:片持ち梁形式,高さ(スパン)=1.2m,断面32cm×32cm,軸力=0) |
各試験体の名称とせん断補強筋量などは,以下のとおりである(詳しい実験諸元については,参考文献[1]を参照されたい).
- S20試験体:D6−SD295A@45mm,pw=0.47%(主鉄筋:D13−SD295A,ps=2.5%)
- S10試験体:φ6−SR235@330mm,pw=0.06%(主鉄筋:D13−SD295A,ps=2.5%)
ここでは,通例の載荷方法に従い,主鉄筋の初期降伏時変位δy以降,その整数倍の変位を数回(ここでは3回ずつ)正側と負側を行き来させ(+1δy〜-1δyを3回繰返し,+2δy〜-2δyを3回繰返し,+3δy〜-3δyを3回繰返し,+4δy〜-4δy
……),崩壊するまで柱頭(上端)変位を逐次増加させるものである.このような載荷方法は,正確に言えば,「降伏変位整数倍漸増による交番正負等変位制御型繰返し載荷」と呼ぶことができよう.
そして,図1の両試験体を概観すると,最大耐力はほぼ同じであるが,せん断補強の程度により,繰返し挙動と靭性が異なることを見て取ることができる.一方,ひび割れパターンと破壊過程(破壊モード)も全く異なる様相となり,次のようにまとめられる.
- S20試験体:曲げ破壊
基部に塑性ヒンジを形成し,健全な曲げ破壊を呈する.基部のかぶりコンクリート剥落後も帯鉄筋による拘束によって,穏やかな終末となっている.
- S10試験体:曲げ降伏後せん断破壊
軸方向筋の初期降伏後,塑性ヒンジの形成により荷重を保持していたが,?=4以降の載荷過程において斜めひび割れが進展し,せん断破壊によって崩壊した.
すなわち,S20試験体が十分な耐震性を有し,S10試験体は,これに比べてせん断補強が不十分なるが故に,靭性が劣る結果となった.
ここで,図中に記した曲げせん断耐力比と変位靭性率?は,柱部材の重要な耐震性指標となるが,これらは次のように定義される(式(1)の両耐力は,断面耐力ではなく,柱頭の水平荷重によって表されている).
| 曲げせん断耐力比=せん断耐力/曲げ耐力 |
|
(1) |
| 部材靭性率?=終局変位δu/降伏変位δy |
|
(2) |
一般に,曲げせん断耐力比が大きいほど,変位靭性率?が向上するが,図中の試験結果は,このことをよく表していると言える. |
2. 繰返し挙動のまとめ
(1) 1サイクルの変形挙動
次に,S15試験体の繰返し載荷実験の実験結果を参照して,図2のようにまとめた.図(a)の実線は,繰返し挙動のうち,正側と負側のピーク値を連ね,骨格曲線(包絡線)として表し,図(b)は多数の繰返し載荷過程のうち3段階の1サイクル分(1回の繰り返し)を抜出し,正規化して図化したものである.
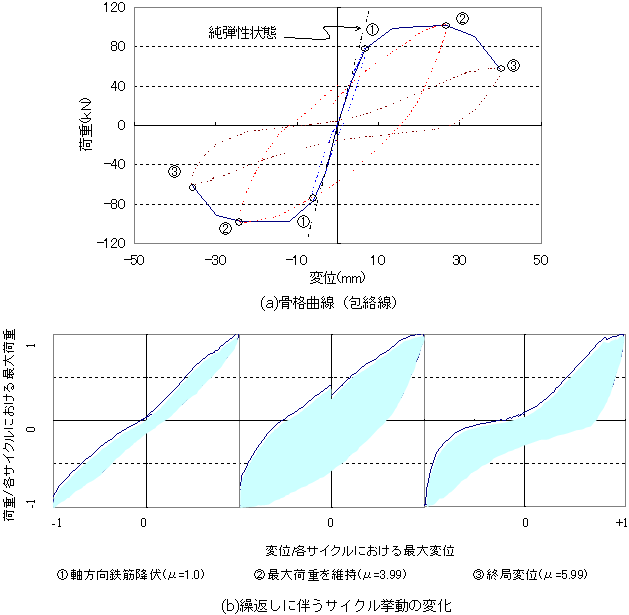 |
図2 繰返し挙動の特徴:骨格曲線と1サイクルの挙動(S15試験体) |
骨格曲線(包絡線)は,ひび割れ発生,初期降伏,最大値などによって,特徴付けられることは,先回詳述したとおりである.図2(b)の履歴性状(サイクル挙動)に関しては,各サイクルの正負ピーク時にて正規化して図示しているので,その形状とループ面積に注目されたい.すなわち,
(1) 軸方向筋降伏時:ほぼ弾性状態(剛性が弾性値と同じで,残留ひずみはほとんどない)を維持している.
(2) 最大荷重時:いわゆる紡錘型のループを呈し,十分なエネルギー消費を観察することができる.
(3) 終局時:部材劣化に伴うS字型のサイクルとなっており,ループ面積が減少していることが分かる.
以上を整理すると,繰返し変位履歴に伴い,等価剛性(原点とピークの勾配)は減少するが,主鉄筋降伏とコンクリートのひび割れ/非線形挙動により,1サイクルのループ面積は大きくなり,動的作用時には減衰性能が高まる.やがては,終末を迎えることになるが,どの程度の変位まで抵抗力の保持と履歴減衰を発揮できるかが,耐震性能の優劣を決することになる.
(2) 1サイクルのモデル化
さて,繰返し挙動のまとめとして,3つの典型的な変形挙動を整理し,図3に模式化した.これらをまとめると,以下のように整理できる.
(a) 紡錘型:
繰返し履歴ループの面積が大きく,十分なエネルギー吸収能力がある.適切な主鉄筋と帯鉄筋の配筋により,理想的な部材特性を達成できる.
(b) 逆S字型:
構造材料の劣化,構造形状,せん断成分の増加により,このような逆S字型の履歴ループを有する.特に原点付近(荷重が正負反転する時),くびれを呈することが特徴である(ピンチ効果とも呼ばれる).紡錘型に比べて履歴ループの面積が小さく,エネルギー吸収能力は劣る.
(c) スリップ型:
打継ぎ面などの滑りにより,荷重反転時に大きな変形(スリップ)を生じる.ループ面積小さく,エネルギー吸収能力はかなり劣る.
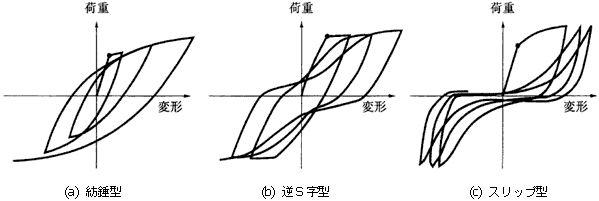 |
図3 典型的な3つ繰返し挙動 |
なお,第1象限の初期の折れ点を黒丸にて示したが,これは初期降伏点(主鉄筋)であり,以降,Bauschiger効果により滑らかな変形挙動となることは3例とも共通し,初期降伏以降に3例の差異が現れると言える.同図は,鉄筋コンクリートの特徴的な繰返し挙動を単純化/模式化し,大略的に説明したものとして理解いただきたい. |
3. 履歴特性のモデル化
以上のような実験的に得られた複雑な実挙動を,今度は,適当な簡略化/理想化により,設計手法/計算ツールに使用可能なモデルに置換えなければならない.繰返し挙動(復元特性)を特徴付ける履歴特性を紹介する.
 |
図4 復元力特性の特徴とモデル化:非劣化モデル/劣化モデル |
復元力特性のモデル化として,骨格曲線とループ特性を組合わせて,図4に2つ例示した.このような復元力特性は,正側での弾性から始まり,降伏(載荷),除荷,(反転して)負側の載荷,除荷,(再度反転して)正側での再載荷,除荷のように,複雑な様相を呈するが,図4の左右両図にてこの一連の展開を辿ってもらいたい(ここで‘載荷’(loading)とは,降伏状態を示し,bi-linearの場合,第2勾配上にあることを意味している).
図4左図は,骨格曲線がbi-linear,履歴則は非劣化モデルであり,除荷は常に弾性時の剛性(初期剛性)と同一であり,最も簡便な繰返しモデルである.右図の場合,tri-linearによる骨格曲線と劣化型の履歴性状を組合せたもの(degrading
tri-linear model)である.劣化型モデルは,除荷時の剛性(戻り勾配)が,それまでの最大変位が大きくなるほど,低下している(寝てくる)ことが特徴的である.
単一の弾塑性材料であれば,‘塑性ヒステリシス’と呼ばれ,いくつかの解析モデルが構築されているが,鉄筋コンクリートはさらに煩雑なモデル化を強いられる. |
4. 数値解析#1:静的繰返し載荷
図5に,骨組み解析ツールを用いて,実験と同様の静的繰返し載荷による静的非線形解析結果(載荷点における水平荷重−水平変位関係)を示した(図(c)は,解析対象の試験体である)。図(a)と(b)は,材料非線形特性のモデル化方法が異なるもので,(a)は材料非線形履歴を考慮したファイバーモデルを用いて,
(b)は折れ線によるM−φ関係を用いるが,図4(b)に示すような劣化モデルによりその復元力特性を与えている。また,図中の太線は実験結果の包絡線を表すものである。
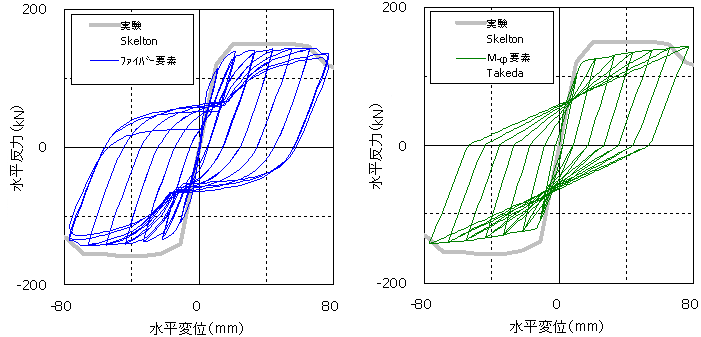
(a) ファイバーモデルによる結果 (b)
M−??(Takedaモデル)による結果 |

|
| 概観図 断面図 |
(c) 解析対象[2]
図5 水平荷重−水平変位履歴[4] |
材料非線形特性のモデル化の違いは,その除荷・再載荷履歴の形状と包絡形状に表れる。ファイバーモデルの結果(図(a))は,除荷・再載荷時の履歴が曲線を描くのが特徴で,包絡形状についても,実験結果をよく模擬できている。一方,M−φ(Takedaモデル)による結果は,部材に与えたM−φ関係の形状が,除荷・再載荷履歴の形状と包絡形状に強く反映されることとなる。すなわち,骨格曲線ならびに復元力特性の選択が肝要となる。しかし,いずれの結果も,除荷時の剛性は初期勾配よりも小さく,さらに変形が大きくなるに伴い除荷時の剛性が低下する,鉄筋コンクリート部材特有の挙動を表すことができている。 |
5. 数値解析#2:動的応答解析
図6に示す結果は,同図(c)に示す震動台実験を模擬したもので,橋軸方向に最大400Gal(=4m/sec2)程度の地震動により加振されたものである。地震動には,1983
年の日本海中部地震において八郎潟干拓堤防上で記録された加速度波形(堤軸直角方向成分)の時間軸を1/2
に縮めた波形が用いられている。また,端部柱上の可動(ローラー)支承の摩擦力は非常に小さいため,桁の慣性力の大部分が橋梁模型中央部のRC
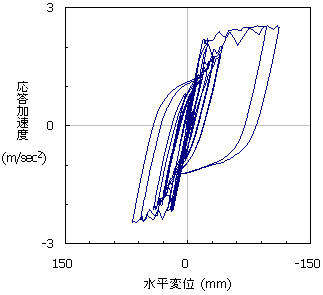
橋脚に伝達される構造系となる。よって,解析は,中央のRC橋脚のみを取り出し,桁重量を橋脚天端に集中質量として与えて実施した。図(a)と(b)は,前述の図5と同様に,材料非線形特性のモデル化方法が異なるものであるが,震動台実験においては,橋脚天端に作用する力は地震による慣性力であるため,水平荷重−水平変位関係に相当するものとして,橋脚天端の応答加速度と水平変位を示している。
 |
 |
(a) ファイバーモデルによる結果 |
(b) M−??(Takedaモデル)による結果 |

震動台 |

橋脚
(c) 解析対象[3]
図6 橋脚天端位置の水平加速度−水平変位履歴 |
図(a)と(b)を見ると,除荷・再々荷時の履歴形状と包絡線形状については図5での考察と同様の特徴をもつが,両者とも,ランダムな地震動に起因する特徴が読み取れる。大きな振幅は高々1,2波程度であり,その後,中小振幅が継続し,図中の原点付近に集中する履歴が生じる。このように,実際の地震動の元では,初期に数回の大きな振幅を受け,その後に小振幅が継続することがあり,静的繰返し実験のような,徐々に振幅が増大する挙動とはならないことに,注意が必要である。 |
使用ツールの紹介
部材の非線形挙動の数値解析を行うにあたり,骨組み解析による手法を用いており,ここではUC-win/FRAME(3D)(株式会社フォーラムエイト)を利用した。部材の非線形挙動を求めるには,有限要素法などにより詳細な解析ツールもあるが,梁/柱などの棒部材が対象の場合は,ファイバーモデルを用いることで,より簡便に,かつ,大規模な構造系の非線形解析が可能となる。また,本ツールは,ファイバーモデルの要となる,コンクリートや鋼材の材料非線形履歴モデルが豊富なのが特徴であると同時に,第3講までに利用した断面特性の計算機能も併せ持っている。研究・実務,土木・建築,様々な用途に活用できるツールである。以下は,実行画面の例である。
※詳しくは,ホームページ(http://www.forum8.co.jp/product/ucwin/frame3d/ucwin-frame3d-3.htm)を参照されたい。
参考文献
[1]吉川弘道:『もっと知りたいコンクリート講座』,http://c-pc8.civil.tcu.ac.jp/RC/ciber/act/act_a.htm
電子サイバー講座>研究室活動>主要構造実験の報告書
[2]星隈順一,運上茂樹,川島一彦,長屋和宏:載荷繰り返し特性と塑性曲率分布に着目した曲げ破壊型鉄筋コンクリート橋脚の塑性変形性能とその評価方法,構造工学論文集,Vol.4A,1998.3,土木学会
[3]土木学会:阪神淡路大震災の被害分析に基づくコンクリート構造物の耐震性能照査方法の検証−解析手法の適用と比較−,
コンクリート技術シリーズ49, 土木学会, 2002.12
[4]高梨和光,青戸拡起:3次元動的解析法を用いた耐震性能照査方法に関する考察,第8回地震時保有耐力法に基づく橋梁等構造の耐震設計に関するシンポジウム講演論文集,2005.2 |








