 |
|
|
先般ご報告の通り、xpswmm2D(xp2Dモジュール)はFEMA(アメリカ合衆国連邦緊急事態管理庁)の認定を受け、自然洪水保険計画NFIP(the
National Flood Insurance Program)における二次元モデリング及びハザードマッピングに適用されることになりました。この背景としては、NFIPの目的とソフトウェア及び解析エンジンの性能が一定の評価を受けたことに起因します。
FEMA認定の要因としては、1D/2D統合解析の有用性やマッピング機能が優れていること等が挙げられますが、主因としては高精度な二次元解析が評価されたことにあると言えます。xpswmm2Dによりこのような高精度のシミュレーションが実現できる理由としては、流体の挙動を表現する支配方程式と数値解析ロジックが他の洪水解析コードに比して優れていることから裏付けられます。
すなわち、xpswmmの二次元解析エンジンでは、洪水解析等では支配方程式の簡易化から一般に無視することが多い様々な項を考慮した厳密な解法としており、複雑な乱流現象まで表現できることから、複雑な挙動をシミュレートできます。河川や湖沼、海洋での高潮や津波、洪水などにおける水の挙動の多くは、水深方向に比べて波長が非常に長いため、浅水波長流れ(shallow
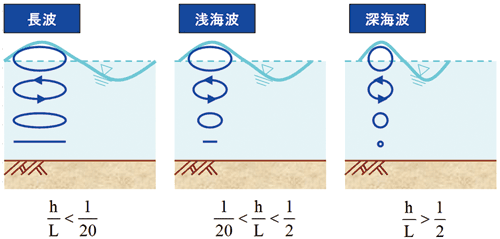
water long wave flow)として取り扱われます。この浅水波長流れは、三次元のNavier-Stokes方程式及びEuler連続式において、速度の鉛直成分を無視し、鉛直方向の圧力分布を静水圧分布に従うと仮定して、運動方程式及び連続式を水深方向に海底から水面までに流速を積分平均することにより導出されます。つまり、波長の長い波の運動では、水中の圧力は静水圧分布に近似でき、水平方向の流速成分は鉛直方向にほぼ一様な分布であるとした長波近似による浅水理論により厳密な運動方程式が導かれます。波高hと波長Lとの比である相対水深h/Lにより、長波及び浅海波、深海波に区分され、深海波では、波による水粒子の運動は水底まで達しませんが、長波の場合には水面から水底までほぼ一様の運動となります(図2)。
 |
|
 |
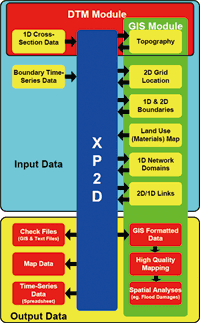
■図1
二次元解析エンジンを含む
xpswmmのシステム構造 |
|
■図2 長波の定義 |
これにより、厳密な浅水長波方程式は、非定常項、圧力項(静水圧分布)、コリオリ力の項、移流項、摩擦項、水平渦動粘性項、等の非線形性を含んだ非線形長波で定式化されます。一方、深海波では水底の影響を受けないため、移流項や摩擦項等を無視することができ、線形長波として表されます(図3)。
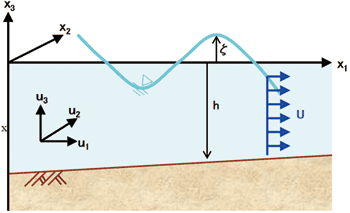 |
| ■図3 座標系 |
この厳密な浅水長波方程式において、一般に様々な簡易化が図られます。河川解析では簡易化のためコリオリ力の項を無視され、洪水解析では渦動粘性項やコリオリ力の項等が無視されることがあります。これに対し、xpswmmでは支配方程式の簡易化を図らず、あらゆる項を考慮しており、差分法における計算スキームとしてはADI法により陰的に解法しているため、浸水現象に特化せず様々な水理現象を高精度で解くことができ、この点が高く評価されたと言えます。
 |
|
 |
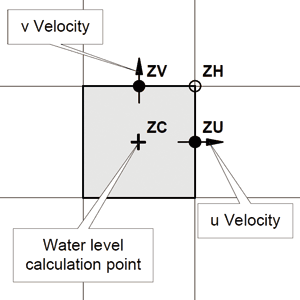
| ■図4 計算スキーム |
|
xpswmmセミナー
●日時 : 2011年 8月 3日(水) 9:30〜16:30 ●参加費 : \15,000 (1名様・税込 \15,750)
●本会場 : フォーラムエイト東京本社 GTタワーセミナールーム TV会議システムにて東京・大阪・名古屋・福岡・仙台にて同時開催 |
|
|
| (Up&Coming '11 盛夏の号掲載) |
 |
|







>> 製品総合カタログ

>> プレミアム会員サービス
>> ファイナンシャルサポート
|








