
|
|
|
â—ڈى²کىŒى—گ
م€€UC-win/FRAME(3D) Ver 4.00.00ىک ى£¼ëگœ ىœ ىƒپ ê°œى • ي•ëھ©ى€ 다ىŒىک 3ى گى…니다.
- ى ˆى گ ى§ˆëں‰ىک ي‘œيک•ى‹ ى…ë ¥
- ى´ˆê¸° ë‹¨ë©´ë ¥
- 기ي•ک ê°•ى„±ى„ ê³ ë ¤ي•œ ê³ ىœ ê°’ ي•´ى„
â—ڈى ˆى گ ى§ˆëں‰ىک ي‘œيک•ى‹ ى…ë ¥
م€€ى ˆى گى—گ ى§ˆëں‰ى„ ى§پى ‘ 부ى—¬ي• ىˆک ىˆëڈ„ë، ëگکى—ˆىٹµë‹ˆë‹¤(그림1). 1ê°œىک ى ˆى گى—گ 대ي•´ى„œ, 병ى§„ë°©ي–¥ 3ى„±ë¶„(ى „ى²´ ى¢Œي‘œê³„ىک X, Y, Z)ê³¼ يڑŒى „ ê´€ى„± ى§ˆëں‰ 3ى„±ë¶„(ى „ى²´ ى¢Œي‘œê³„ىک Xى¶•يڑŒى „, Yى¶•يڑŒى „, Zى¶•يڑŒى „)ىک ي•©ê³„ 6ى„±ë¶„ى„ 부ى—¬ي•©ë‹ˆë‹¤. ê°€ë،œë،œ 6ى—´, ى„¸ë،œë،œ ëھ¨ë“ ى ˆى گى´ ëٹکى–´ى„ ي‘œيک•ى‹ىœ¼ë،œ 부ى—¬ي•ک므ë،œ, ë³µى‚¬مƒ»ë¶™ى´ê¸°ê°€ 간단ي•©ë‹ˆë‹¤.
م€€ë¶€ى¬ى—گى„œ ى ˆى گ ى§ˆëں‰ى„ ى‚°ى¶œى‹œي‚¤ëٹ” 것ëڈ„ ê°€ëٹ¥ي•©ë‹ˆë‹¤. [부ى¬ى—گى„œ 계ى‚°]ى´ë¼ê³ ي•کëٹ” 버يٹ¼ى„ 누르면 ىگëڈ™ ى‚°ى¶œëگ©ë‹ˆë‹¤. ى´ 계ى‚° 방법ى€ Lumped
Mass(ى§‘ى¤‘ ى§ˆëں‰)ى…니다. 구ى²´ى پىœ¼ë،œëٹ”, 부ى¬ ى§ˆëں‰ىک ى ˆë°کى„ ي•œىھ½ىک ى ˆى گىœ¼ë،œ 배분ي•©ë‹ˆë‹¤. ى ˆى گى—گ ى ‘ى†چëگکى–´ ىˆëٹ” ëھ¨ë“ 부ى¬ ى§ˆëں‰ىک ى ˆë°کى„ ى§‘계ي•کى—¬, ê·¸ ى ˆى گىک ى§ˆëں‰ىœ¼ë،œ ي•©ë‹ˆë‹¤. ى´ ى§‘ى¤‘ ى§ˆëں‰ë²•ى€ ى •ë°€ëڈ„ê°€ ى¢‹ى§€ ى•ٹى€ 것ىœ¼ë،œ ى•Œë ¤ى ¸ ىˆى§€ë§Œ, ى‚¬ê³ ë°©ى‹ى´ ى‹¬ي”Œي•ک다ëٹ” 것과, 내부ى پىœ¼ë،œëٹ” ى§ˆëں‰ 매يٹ¸ë¦ىٹ¤ê°€ 대ê°پ ى„±ë¶„만ىœ¼ë،œ ëگکى–´ ي–‰ë ¬ 계ى‚°ى´ ىڑ©ى´ي•ک다ëٹ” ى گىœ¼ë،œë¶€ي„° ىگى£¼ ى´ىڑ©ëگکê³ ىˆىٹµë‹ˆë‹¤. |
|
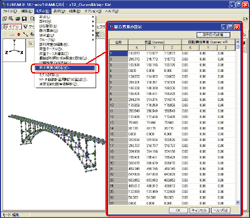
▲그림1م€€ى ˆى گ ى§ˆëں‰ىک ى…ë ¥ ي™”ë©´ |
م€€ى¢…ëک까ى§€ëٹ” 1ى ˆى گ만ىک ê°•ى²´ىڑ”ى†Œë¥¼ ى‘ى„±ي•کى—¬ ى§ˆëں‰ى„ 부ى—¬ي•کëٹ” 방법ى—گ ىکي•´ ى ˆى گ ى§‘ى¤‘ ى§ˆëں‰(ى§ˆى گ)ى„ ى„¤ى •ي–ˆى—ˆىٹµë‹ˆë‹¤. ê·¸ë ‡ê¸° 때문ى—گ ê°•ى²´ىڑ”ى†Œë¥¼ ى‘ى„±ي•کëٹ” 번거ë،œى›€ى´ ىˆë‹¤ëٹ” ى گ, 다ىˆکىک ى§ˆى گى„ ى •ىکي• ي•„ىڑ”ê°€ ىˆى„ ë•Œëٹ” ê°•ى²´ىڑ”ى†Œىک يژ¸ى§‘ ي™”ë©´ى„ ëھ‡ë²ˆى”©ى´ë‚ک يک¸ى¶œي•کى§€ ى•ٹىœ¼ë©´ ى•ˆëگکëٹ”다ëٹ” ى گى´ 불يژ¸ي–ˆى—ˆىٹµë‹ˆë‹¤. ى´ë²ˆىک ى ˆى گ ى§ˆëں‰ىک ي‘œيک•ى‹ ى…ë ¥ى—گ ىکي•´, ى´ëں¬ي•œ 번거ë،œىڑ´ ى‘ى—…ى´ ى—†ى–´ى§‘니다. ى§ˆى گى„ ىœ„ي•´ى„œ ê°•ى²´ىڑ”ى†Œë¥¼ ى¤€ë¹„ي• ي•„ىڑ”ëڈ„ ى—†ى–´ى§‘니다.
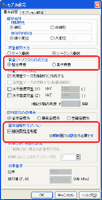
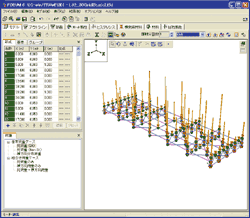
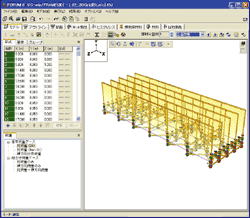
م€€ى ˆى گ ى§ˆëں‰ى„ ي‘œيک•ى‹ىœ¼ë،œ 부ى—¬ي•œ ê²½ىڑ°, ي”„ë،œê·¸ë¨ى´ ىگëڈ™ ى‚°ى¶œي•کëٹ” ى‚¬ي•کى¤‘ى´ë‚ک ىˆکيڈ‰ ى§„ëڈ„ ي•کى¤‘ى—گëڈ„ ë°کىکپى‹œي‚¬ ىˆک ىˆىٹµë‹ˆë‹¤. ëھ¨ëچ¸ ى„¤ى • ي™”ë©´ى—گى„œ [ى§‘ى¤‘ ى§ˆëں‰]ى„ ى„ يƒي•کë©´, ى‚¬ي•کى¤‘ى´ë‚ک ىˆکيڈ‰ ى§„ëڈ„ ي•کى¤‘ى´ ى ˆى گىœ¼ë،œىک ى§‘ى¤‘ ي•کى¤‘ىœ¼ë،œىچ¨ ى¬ي•کëگ©ë‹ˆë‹¤(그림2, 그림3). ëھ¨ëچ¸ ى„¤ى • ي™”ë©´ى—گى„œ [ى •ي•© ى§ˆëں‰]ى„ ى„ يƒي•کë©´, 부ى¬ë،œىک 분يڈ¬ ي•کى¤‘ىœ¼ë،œ ى¬ي•کëگ©ë‹ˆë‹¤(그림2, 그림4).
 |
|
 |
|
 |
▲그림2م€€ى§ˆëں‰ 매يٹ¸ë¦ىٹ¤ىک
ى‘ى„± 방법 ىکµى…کê³¼
ê³ ىœ ي•´ى„ ىکµى…ک |
|
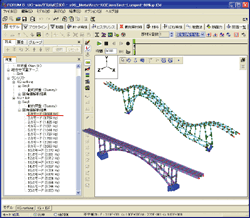
▲그림3م€€ى§‘ى¤‘ ى§ˆëں‰ë²•ى—گ ىکي•œ ى‚¬ي•کى¤‘
(ى ˆى گىœ¼ë،œىک ى§‘ى¤‘ ي•کى¤‘) |
|
▲그림4م€€ى •ي•© ى§ˆëں‰ë²•ى—گ ىکي•œ ى‚¬ي•کى¤‘
(부ى¬ë،œىک 분يڈ¬ ي•کى¤‘) |
م€€ëچ§ë¶™ى—¬ ë§گي•کë©´ [ى •ي•© ى§ˆëں‰]ى€ 본 ي”„ë،œê·¸ë¨ى´ ى´ˆيŒگ부ي„° ى±„ىڑ©ي•کê³ ىˆëٹ” ى§ˆëں‰ 매يٹ¸ë¦ىٹ¤ىک 구ى„±ë²•ى…니다. [ى •ي•© ى§ˆëں‰]ى€ ىڑ”ى†Œë‚´ىک ê°€ى†چëڈ„ 분يڈ¬ë¥¼ ë³€ىœ„ ي•¨ىˆکىک 2يڑŒ 미분ى—گ ىکي•´ى„œ 구ي•کê³ , 그것ى—گ ىکي•œ ê´€ى„±ë ¥ 분يڈ¬ë¥¼ 구ي•کëٹ” 방법ىœ¼ë،œ, Consistent
Massë،œ 불리ىڑ°ê³ ىˆىٹµë‹ˆë‹¤. ى´ ى¼ë³¸ى–´ى—گ ي•´ë‹¹ي•کëٹ” 번ى—ى–´ëٹ”, ى •ي•© ى§ˆëں‰, 분يڈ¬ ى§ˆëں‰, ى،°ي™” ى§ˆëں‰ê³¼ ê°™ى´ ى—¬ëں¬ê°€ى§€ ىˆى§€ë§Œ, ى–´ëٹگ것ëڈ„ ê°™ى€ ى§ˆëں‰ 매يٹ¸ë¦ىٹ¤ىک 구ى„±ë²•ى„ 가리ي‚µë‹ˆë‹¤. ى •ي•© ى§ˆëں‰ë²•ى€, ى پى€ ى ˆى گىˆکë،œ 다ىگىœ ëڈ„ىک ى§„ëڈ™ يٹ¹ى„±ى„ ى ˆى ˆي•ک게 ë‚کيƒ€ë‚¼ ىˆک ىˆىœ¼ë©°, ى§‘ى¤‘ ى§ˆëں‰ë³´ë‹¤ëڈ„ ى •ë°€ëڈ„ê°€ 높ى€ 답ى„ ى–»ê¸° ى‰½ë‹¤ê³ ي•کëٹ” ى´ى گى´ ىˆىٹµë‹ˆë‹¤. 단, 본 ي”„ë،œê·¸ë¨ىک ى •ي•© ى§ˆëں‰ 매يٹ¸ë¦ىٹ¤ëٹ” 계ى‚°ë¶€ى•ˆى—گى„œ ىگëڈ™ى پىœ¼ë،œ ى‚°ى¶œëگکê³ ىˆىœ¼ë¯€ë،œ 구ى²´ى پى¸ ىˆکى¹ک를 ي™•ى¸ي• ىˆک ëٹ” ى—†ىٹµë‹ˆë‹¤. ê·¸ë ‡ê¸° 때문ى—گ, ى§„ëڈ™ يٹ¹ى„±ى„ ي‘œيک„ي• ىˆک ىˆëٹ” ى •ëڈ„ë،œ ى¶©ë¶„ي•œ ى ˆى گىˆک를 ê°€ى§€ê²Œ ي•کى—¬, ى§‘ى¤‘ ى§ˆëں‰ë²•ى—گ ىکي•œ ى ˆى گ ى§ˆëں‰ىک ى‚°ى¶œى„ ي•´ë‘گë©´, ê°پ ى ˆى گ ى§ˆëں‰ى„ 리يڈ¬يٹ¸ë،œ ى¶œë ¥ي•کëٹ” 것ى´ ê°€ëٹ¥ي•©ë‹ˆë‹¤.
م€€ى§‘ى¤‘ ى§ˆëں‰ë²•, ى •ي•© ى§ˆëں‰ë²•ىک ى–´ëٹگ것ى„ ى´ىڑ©ي•´ëڈ„ ëھ¨ëچ¸ ى „ى²´ىک ى§ˆëں‰ى€ ê°™ى•„ى§‘니다.
â—ڈى´ˆê¸° ë‹¨ë©´ë ¥
م€€ë¶€ى¬ى—گ ى´ˆê¸° ë‹¨ë©´ë ¥ى„ ى„¤ى •ي• ىˆک ىˆëڈ„ë، ëگکى—ˆىٹµë‹ˆë‹¤(그림5). 부ى¬ë؟گ만 ى•„니ë¼, ىٹ¤ي”„ë§پىڑ”ى†Œى—گëڈ„ 부ى—¬ي• ىˆک ىˆىٹµë‹ˆë‹¤. ى´ˆê¸° ë‹¨ë©´ë ¥ى´ë€ ي•کى¤‘ى´ ى¬ي•کëگک기 ى „ىک ى´ˆê¸° ى‘ë ¥ ىƒپيƒœë¥¼ ي‘œيک„ي•ک기 ىœ„ي•œ يکى…니다. 부ى¬ë¼ë©´, 부ى¬ ى¬ë‹¨ى—گى„œىک يœ¨ëھ¨ë©کيٹ¸, ى „ë‹¨ë ¥, ى¶•ë ¥ى„ 부ى—¬ي•©ë‹ˆë‹¤. ىٹ¤ي”„ë§پىڑ”ى†Œë¼ë©´, ىٹ¤ي”„ë§پىڑ”ى†Œىک ىڑ”ى†Œ ى¢Œي‘œê³„ى—گ ىˆى–´ى„œىک xlë°©ي–¥, ylë°©ي–¥, zlë°©ي–¥, ê°پê°پىک ى¶•يڑŒى „ىک يڑŒى „ë ¥(ëھ¨ë©کيٹ¸)ى„ 부ى—¬ي•©ë‹ˆë‹¤. ى´ي•ک, ى„¤ëھ…ى„ 간단ي•ک게 ي•ک기 ىœ„ي•´ 부ى¬ى—گ ى°©ى•ˆي•کى—¬, ىٹ¤ي”„ë§پىڑ”ى†Œë¥¼ ىƒëµي•©ë‹ˆë‹¤.
م€€ي•´ى„ى„ ى‹œى‘ي•ک기 ى „ىک 부ى¬ى—گ ىƒê¸°ê³ ىˆëٹ” ë‹¨ë©´ë ¥ ىƒپيƒœë¥¼ 부ى—¬ي•ک기 때문ى—گ, ى´ˆê¸° ë‹¨ë©´ë ¥ى—گ ىکي•œ ى§€ى گ ë°کë ¥ى€ ىƒê¸°ى§€ ى•ٹىٹµë‹ˆë‹¤. ى§€ى گ ë°کë ¥ى€ ي•کى¤‘ى´ ى¬ي•کëگکى—ˆى„ ë•Œى—گ ى²کىŒ ىƒê¹پ니다. ىکˆë¥¼ 들면, ëھ¨ëچ¸ىک ى‚¬ي•کى¤‘ ىƒپيƒœë¥¼ ى´ˆê¸° ë‹¨ë©´ë ¥ى—گ ى§€ى •ي•کë©´, ىµœى´ˆىک 1ىٹ¤ي…ى§¸ىک 계ى‚° ê²°ê³¼ى—گëٹ” ى‚¬ي•کى¤‘ ë°کë ¥ى´ يڈ¬ي•¨ëگکى§€ ى•ٹىٹµë‹ˆë‹¤. |
|
▲그림5م€€ى´ˆê¸° ë‹¨ë©´ë ¥ىک ى…ë ¥ ي™”ë©´ |
م€€ë§ˆى°¬ê°€ى§€ë،œ, ى´ˆê¸° ë‹¨ë©´ë ¥ى„ 부ى—¬ي•œ ىƒپيƒœى—گى„œëٹ” ى ˆى گى—گ ë³€ىœ„ëٹ” ىƒê¸°ى§€ ى•ٹىٹµë‹ˆë‹¤. ى´ê²ƒى€ ى´ˆê¸° ë‹¨ë©´ë ¥ى„ ىƒê¸°ê²Œ ي•کëٹ” ي•کى¤‘ى´ ى¬ي•کëگœ ي•´ى„ ê²°ê³¼ى¤‘, ى ˆى گ ë³€ىœ„를 무ى‹œي•کê³ ë‹¨ë©´ë ¥ë§Œى„ ى¶”ى¶œي•کى—¬ ى´ˆê¸° ىƒپيƒœë،œ ي•ک기 때문ى…니다. ê·¸ëں¬ë‚ک, 부ى¬ ë³€ىœ„ëٹ” ىƒê¹پ니다. ى´ê²ƒى€ ى´ˆê¸° ë‹¨ë©´ë ¥ى´ 부ى¬ë‚´ى—گ ى،´ى¬ي•کê³ ىˆë‹¤ê³ ê°€ى •ي•کê³ ىˆىœ¼ë¯€ë،œ 그것ى—گ ىکي•œ 부ى¬ë‚´ ë³€ىœ„ëٹ” ë°œىƒي•کê³ ىˆë‹¤ê³ ىƒê°پي•ک기 때문ى…니다. ى ˆى گ ë³€ىœ„ëٹ” ىƒê¸°ى§€ ى•ٹê³ , 부ى¬ ë³€ىœ„ê°€ ىƒê¹€ى—گ ë”°ë¼, i단과 j단ى—گى„œëٹ” 부ى¬ ë³€ىœ„ëٹ” ى œë،œê°€ ëگ©ë‹ˆë‹¤.
م€€ى´ˆê¸° ë‹¨ë©´ë ¥ىک ى„¤ى • ي™”ë©´ى—گëٹ”, ى–´ë–¤ ي•کى¤‘ ى¼€ى´ىٹ¤ë¥¼ ى„ يƒي•کى—¬ ي”„ë ˆى„ 계ى‚°ى„ ي•کëٹ” 버يٹ¼ى´ ىˆىٹµë‹ˆë‹¤. ê·¸ 버يٹ¼ى„ 누르면, ê·¸ ي•کى¤‘ ى¼€ى´ىٹ¤ى—گ 대ي•´ى„œ يƒ„ى„± ي•´ى„ى„ ى‹¤ى‹œي•کى—¬, i단과 j단 ىœ„ى¹کى—گى„œىک ë‹¨ë©´ë ¥ى„ ى´ˆê¸° ë‹¨ë©´ë ¥ىœ¼ë،œىچ¨ ى±„ىڑ©ي•©ë‹ˆë‹¤. ى´ى™€ ê°™ى´, ى¬ë‹¨ ىœ„ى¹کى—گى„œىک ë‹¨ë©´ë ¥ى„ ى±„ىڑ©ي•ک기 때문ى—گ, 부ى¬ 내부ىک ë‹¨ë©´ë ¥ 분يڈ¬ ىƒپيƒœëٹ” 무ى‹œëگ©ë‹ˆë‹¤. ë”°ë¼ى„œ, 분يڈ¬ ي•کى¤‘ى´ë‚ک 부등 분يڈ¬ ي•کى¤‘등ىک 부ى¬ ي•کى¤‘ى„ ى¬ي•کي•œ ي•کى¤‘ ى¼€ى´ىٹ¤ىک ë‹¨ë©´ë ¥ 분يڈ¬ ىƒپيƒœى™€, 그것ى„ ى´ˆê¸° ë‹¨ë©´ë ¥ىœ¼ë،œىچ¨ ى±„ىڑ©ي–ˆى„ ë•Œىک ىƒپيƒœى™€ëٹ” ى™„ى „ي•ک게 ى¼ى¹کي•کى§€ ى•ٹىٹµë‹ˆë‹¤. ى´ ىک¤ى°¨ë¥¼ ى‘게 ي•ک기 ىœ„ي•´ى„œëٹ”, ى ˆى گ ي•کى¤‘ى„ ى¬ي•کي•œ ي•کى¤‘ ى¼€ى´ىٹ¤ë¥¼ ى„ يƒي•کë“ ê°€, يک¹ى€ ى ˆى گى„ ë§ژى´ ى·¨ي•œ ëھ¨ëچ¸(부ى¬ىک 분ي• ى„ ى„¸ى„¸ي•ک게 ي•œ ëھ¨ëچ¸)ى„ ى‘ى„±ي•کى—¬ ى£¼ى‹ى‹œىک¤. 다른 ي”„ë،œê·¸ë¨ى—گ ىکي•´ ى–»ى–´ى§„ ë‹¨ë©´ë ¥ى„ ى´ˆê¸° ë‹¨ë©´ë ¥ىœ¼ë،œىچ¨ ى…ë ¥ي• ë•Œëڈ„ ëڈ™ى¼ي•کë‹¤ê³ ë§گي• ىˆک ىˆىٹµë‹ˆë‹¤.
â—ڈ기ي•ک ê°•ى„±ى„ ê³ ë ¤ي•œ ê³ ىœ ê°’ ي•´ى„
م€€ê³ ىœ ê°’ ي•´ى„ى€ ê°•ى„± 매يٹ¸ë¦ىٹ¤[K]ى™€ ى§ˆëں‰ 매يٹ¸ë¦ىٹ¤[M]ى—گ ىکي•´,
م€€م€€م€€|[K]ï¼چد‰2[M]|ï¼0
ى„ ي’€ى–´ى„œ ê³ ىœ ى§„ëڈ™ىˆک د‰ë¥¼ 구ي•©ë‹ˆë‹¤. ى¢…ëک까ى§€ëٹ”, ê°•ى„± 매يٹ¸ë¦ىٹ¤ى—گëٹ” ى„ يک• يƒ„ى„±ىک ê°•ى„± 매يٹ¸ë¦ىٹ¤[K0]를 ى´ىڑ©ي–ˆى—ˆىٹµë‹ˆë‹¤([K]= [K0]). ى´ë²ˆë¶€ي„° 기ي•ک ê°•ى„± 매يٹ¸ë¦ىٹ¤[KG]ëڈ„ ê³ ë ¤ي• ىˆک ىˆىٹµë‹ˆë‹¤. 기ي•ک ê°•ى„±ى„ ê³ ë ¤ي•œ ê²½ىڑ°ëٹ” ىœ„ ى‹ىک [K]ëٹ”, [K]=
[K0]+[KG]ê°€ ëگ©ë‹ˆë‹¤. ëھ¨ëچ¸ ى„¤ى • ي™”ë©´ىک [ê³ ىœ ê°’ ي•´ى„ ىکµى…ک]ى—گى„œ ى§€ى •ي•©ë‹ˆë‹¤. [KG]ى„ ى‘ى„±ي•ک기 ىœ„ي•´ى„œ ى´ˆê¸° ë‹¨ë©´ë ¥ىک ى„¤ى •ى´ ي•„ىڑ”ي•©ë‹ˆë‹¤.
م€€ى œي’ˆ ى²¨ë¶€ىک ىƒکي”Œ ëھ¨ëچ¸[s06__MetalArch.f3d](ê°•ى•„ى¹کêµگ)를 ى´ىڑ©ي•œ ىکˆى—گى„œëٹ”, 기ي•ک ê°•ى„±ى„ ê³ ë ¤ي•کى§€ ى•ٹëٹ” ê²½ىڑ°ىک ê³ ىœ ى§„ëڈ™ىˆک 0.683Hz, 기ي•ک ê°•ى„±ى„ ê³ ë ¤ي•œ ê²½ىڑ°ëٹ” 0.664Hzê°€ ëگکى–´, 기ي•ک ê°•ى„±ى„ ê³ ë ¤ي•کëٹ” 것ى´ ê³ ىœ ى§„ëڈ™ىˆکëٹ” ى•½ 3%ى •ëڈ„ ى‘게 ëگکى—ˆىٹµë‹ˆë‹¤(그림6). ê³ ىœ ى£¼ê¸°ë،œ 바꾸ى–´ ë§گي•کë©´, ى•½ 3%ى •ëڈ„ ى»¤ى§„다ëٹ” 것ى„ ىک미ي•©ë‹ˆë‹¤. 단, 본 ê²€ي† ى—گى„œëٹ”, ى²¨ى„¤يŒگى´ë‚ک ë³¼يٹ¸ë“±ىک ى¤‘ëں‰ى„ ê³ ë ¤ي•ک기 ىœ„ي•´ى„œ ىƒکي”Œ ëھ¨ëچ¸ىک ê°•ى¤‘ى„ 40%ى •ëڈ„ يپ¬ê²Œ ي•کê³ ىˆىٹµë‹ˆë‹¤. ê³ ىœ ëھ¨ë“œëٹ” 1ى°¨ ëھ¨ë“œ(êµگى¶• ى—대ى¹ 1ى°¨)ى—گ ى°©ى•ˆي•œ ê²°ê³¼ى…니다. [ê°•êµگىک ë‚´ى§„مƒ»ى œى§„ ى„¤ê³„ ê°€ى´ë“œë¼ى¸](ىڑ°ى‚¬ë¯¸ ى¸ ي† 무 يژ¸ى €مƒ»ى¼ë³¸ 강구ى،° يک‘يڑŒيژ¸, 2006ë…„9ى›”, 기يک¸ي† ىڑ°)ىک ى•„ى¹کêµگىک 계ى‚°ë،€ى—گى„œëٹ”, 4~5%ى •ëڈ„ىک ى°¨ى´ê°€ ىƒê¸´ë‹¤ê³ ëگکى–´ ىˆىٹµë‹ˆë‹¤.
 |
▲그림6م€€ê¸°ي•ک ê°•ى„±ى„ ê³ ë ¤ي•œ ê³ ىœ ê°’ ي•´ى„ ê²°ê³¼
م€€م€€ï¼ˆêµگى¶• ى—대ى¹ 1ى°¨ ëھ¨ë“œëڈ„) |
â—ڈ기يƒ€
م€€يŒŒى´ë²„ىڑ”ى†Œ 단면ىک ë©”ى‰¬ 분ي• 방법ى—گ, ى¢…يڑ، 분ي• ىکµى…کى„ ى¶”ê°€ي–ˆىٹµë‹ˆë‹¤. ىکˆë¥¼ 들면, ê°€ë،œë،œ 1분ي• , ى„¸ë،œë،œ 20분ي• ى´ë¼ê³ ي•کëٹ” ë©”ى‰¬ 비ىœ¨ى„ 부ى—¬ي• ىˆک ىˆىٹµë‹ˆë‹¤(그림7). ë©´ë‚´ ي•´ى„ى²کëں¼ ى¼ى¶•ë°©ي–¥ë§Œىک 계ى‚°ى—گى„œëٹ” ë©”ى‰¬ 분ي• ëگœ ى…€ىˆکê°€ ى پى–´ى§€ê¸° 때문ى—گ 계ى‚° ى‹œê°„ىک 단ى¶•ى„ 기대ي• ىˆک ىˆىٹµë‹ˆë‹¤.
 |
| ▲그림7 يŒŒى´ë²„ىڑ”ى†Œ 단면ىک ى¢…يڑ، ë©”ى‰¬ 분ي• |
â—ڈ마ى§€ë§‰ىœ¼ë،œ
م€€ى´ë²ˆىک ê°œى • ë‚´ىڑ©ى€ ëھ¨ë‘گ, ى§€ê¸ˆê¹Œى§€ 다ىˆکىک ê³ ê°ىœ¼ë،œë¶€ي„° ىڑ”ë§ى„ ë°›ى•کëچک 것ى…니다. ي•´ى„ 기ëٹ¥ى—گ ê´€ي•œ ى¤‘ىڑ”ي•œ 기ëٹ¥ ى¶”가를 ي•کىک€ىœ¼ë¯€ë،œ, ى§€ê¸ˆê¹Œى§€ UC-win/FRAME(3D)ىک ى پىڑ©ى„ ë³´ë¥کي•کê³ ىˆى—ˆëچک 구ى،°ë¬¼ىک ي•´ى„ى´ ê°€ëٹ¥ي•ک게 ëگ©ë‹ˆë‹¤. ê¼ ى´ىڑ©ي•کى—¬ ى£¼ى‹ى‹œىک¤.
|
UC-win/FRAME(3D)مƒ»ëڈ™ى پ ي•´ى„ ى„¸ë¯¸ë‚ک
م€€â—ڈى¼ى‹œ ï¼ڑ 2010ë…„ 1ى›” 8ى¼ï¼ˆê¸ˆï¼‰ م€€9ï¼ڑ30~16ï¼ڑ30
م€€â—ڈى°¸ê°€ë¹„ ï¼ڑ \15,000 (ى„¸ê¸ˆيڈ¬ي•¨ \15,750)
م€€â—ڈ본يڑŒى¥ ï¼ڑ يڈ¬ëں¼ى—گى´يٹ¸ ëڈ™ê²½ë³¸ى‚¬ GTيƒ€ى›Œ ى„¸ë¯¸ë‚ک룸
م€€م€€م€€م€€م€€م€€م€€م€€م€€TVيڑŒىک ى‹œىٹ¤ي…œىœ¼ë،œ ëڈ™ê²½مƒ»ىک¤ى‚¬ى¹´مƒ»ë‚کê³ ى•¼مƒ»ي›„ى؟ ىک¤ى¹´ى—گى„œ ëڈ™ى‹œ ê°œىµœ |
|
| â– UC-win/FRAME(3D) Ver 4 릴리ىٹ¤ ىکˆى •ى¼ï¼ڑ2010ë…„1ى›” |
| (Up&Coming '10 ى‹ ë…„يک¸ 게ى¬ï¼‰ |
 |
|







>> گ»•i‘چچ‡ƒJƒ^ƒچƒO

>> ƒvƒŒƒ~ƒAƒ€‰ïˆُƒTپ[ƒrƒX
>> ƒtƒ@ƒCƒiƒ“ƒVƒƒƒ‹ƒTƒ|پ[ƒg
|








