WebLesson:#9
RC部材の終局変位と靭性評価
株式会社 フォーラムエイト 技術サポートグループ |
地震時における鉄筋コンクリート部材は,複雑な繰返し挙動を呈するが,耐震設計に際しては,終局変位もしくは部材靭性率の評価が必要となる.ここでは,RC橋脚を対象として,終局変位の考え方について述べるとともに,部材靭性率の評価方法について説明したい.とくに,変位靭性率については数値シミュレーションにより考察した.最後に,応答塑性率による耐震設計の基本的な手順を示した.
Key Word:終局変位,変位靭性率,RC橋脚,応答塑性率 |
1. RC柱部材の終局変位
曲げ変形δuは,基部(最大曲げモーメント位置)にて降伏した後は,ヒンジ部における塑性回転成分を含むことになるので,次式のように考える(図1),
|
δu=降伏曲率までの変形δy+ヒンジ部の塑性変位δp |
(1) |
この2成分δy,δpは次のように整理できる. |
|
|
 |
(2) |
|
 |
(3) |
ここで,φy,φu,φp=降伏時,終局時,塑性曲率.φp=φu−φy
θp(=φp・Lp)=塑性ヒンジ領域の回転角,Lp =等価塑性ヒンジ長さ
2成分δy,δpに対する式(2)と式(3)の最終項は,設計計算用の近似式としてよく用いられている.ここで,塑性ヒンジによる基部回転角をθp=φp・Lpのように考えるもので,例えば,鉄道構造物等設計標準(略称,鉄道標準)[1]の算定方法を例示する.
これは,上記式(3)を鉄道標準の記号に書直すと,終局時の部材変位δnp(塑性ヒンジによる変位)が次式にて表示される.
|
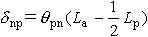 |
(4) |
ここで,塑性ヒンジによる回転角θpnは,具体的に下式にて算出される. |
|
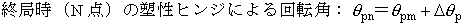 |
(5-1) |
|
 |
(5-2) |
|
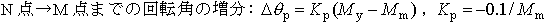 |
(5-3) |
ここで,La=せん断スパン,Lp=等価塑性ヒンジ長,My=降伏時の曲げモーメント,Mm=最大曲げモーメント,pw,pt,kw0=帯鉄筋比(%),引張鉄筋比(%),帯鉄筋強度を考慮する係数
一方,等価塑性ヒンジ長さは,いくつかの実験式が提案されており,通例,断面高さの1〜0.5倍程度となるが,次式のような提案式がよく知られている. |
|
Priestley etal. :Lp=0.08L+0.022dsfy≦0.044dsfy |
(6-1) |
|
道路橋示方書 :Lp=0.2h-0.1D,0.1D≦Lp≦0.5D |
(6-2) |
|
鉄道標準 :Lp=1.0D |
(6-3) |
ここで,L,h=部材高さ,D=断面の径,fy=軸方向筋の降伏強度,ds=軸方向筋の直径である.
式(6-1)は,第1項が柱本体の塑性ヒンジの長さを示し(部材高さの0.08倍),第2項は軸方向筋の基礎部への貫入(tensilestrain
penetration)による影響を表している(軸方向筋の降伏強度と直径に比例).
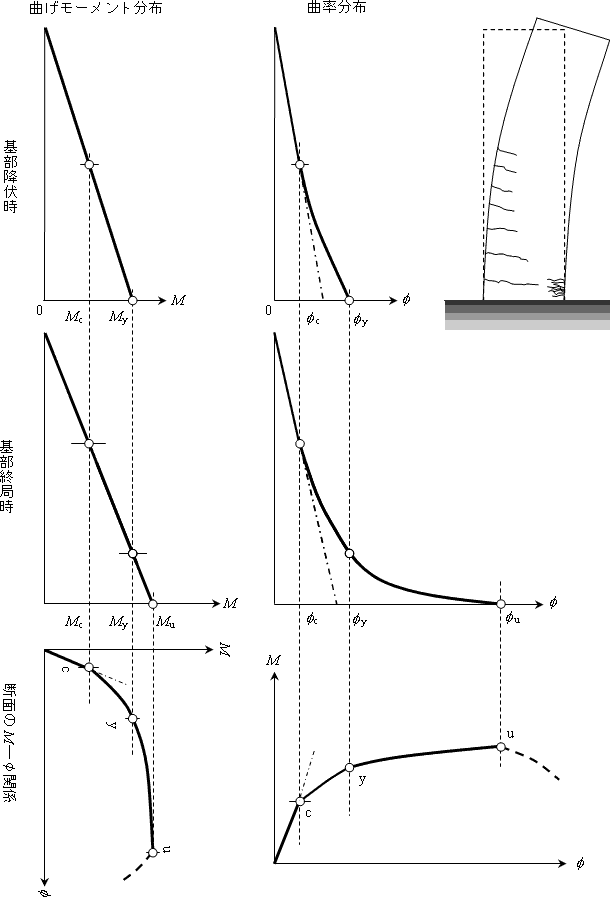 |
図1 柱部材の曲げモーメント分布と曲率分布 |
|
2. 曲率靭性率と変位靭性率の算出
断面靭性と部材靭性とは,初期の降伏以降,耐荷力を保持しながら変形に追随する能力を示すものである.ここでは,終局時の変形(下添え字u:ultimate)を軸方向鉄筋降伏時(添え字y:yield)について除した(正規化した)ものを靭性率(ductility
factor)と称し,基準となる変位量によって,次の3つが定義される.
|
 |
(7) |
RC単柱の場合,μφ>μδとなることが多い.
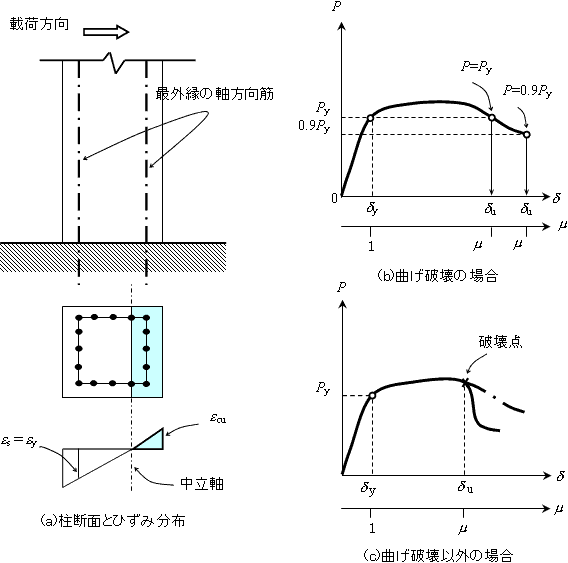 |
図2 部材のP−δ 曲線と降伏変位/終局変位の定義 |
ここで,変位靭性率を例にとり,その分子δyと分母δuの定義を図2によって例示したい.すなわち,δy:引張鉄筋が最初に降伏したときの変位(柱断面は数段の軸方向筋が配されるが,通例,引張側の最外縁の鉄筋を用いる).δu:曲げ破壊の場合,圧縮側最外縁のコンクリートひずみが終局ひずみに達した場合をもって,曲げ終局状態することが多いが,圧縮側最外縁の鉄筋位置におけるコンクリートひずみを用いることもある(図2(a)).
このような定義とは別に,部材のP−δ曲線(包絡線)の様子から,靭性を定義することも多い.例えば,曲げ破壊の場合では,初期降伏時変位δyのときの荷重Pyを,その後の荷重履歴の過程で下回る(もしくは,その90%を下回る)時点をもって,終局とすることも工学的な方法として用いられる(図2(b)).また,せん断破壊,鉄筋の座屈など,唐突な破壊(accidental
failure),想定していない早期の破壊(premature failure)が生じれば,その時点にて終局であることは言うまでない(図2(c)).
このような変位靭性率を具体的に求めると,前述の算定結果,式(2), (3)を用いて,次式にて表される. |
|
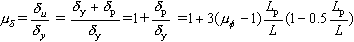 |
(8-1) |
降伏耐力Myから終局耐力Muまでに増加があるときは,下式にて修正される. |
|
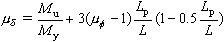 |
(8-2) |
これら式(8)は,曲率靭性率μφから変位靭性率μδを算出するものであるが,耐震設計に際しては,逆に要求靭性率(変位靭性率)からこれを満たす曲率靭性率μφを求めることになり,断面設計での要求性能の一つとなる.これは,例えば,式(8-2)を書き換えて,次のように表現できる. |
|
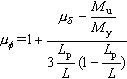 |
(9) |
この場合,部材靭性率μφを必要靭性率(ductility demand)と置き換えて,右辺の諸量を代入して,曲率靭性率μφを求解し,これを満足する断面設計を行うものである.
|
3. 既設橋脚の靭性評価:道路橋T型単柱橋脚
最後に,既設の鉄筋コンクリート橋脚を対象として,1質点系にモデル化し,P-δ関係,靭性評価(部材靭性率)などを試算してみよう.そこで,T型単柱式橋脚(図3の右下部に構造諸元を示した)を基準モデル[2]として採用した(本橋脚は昭和55年に設計されたもので,現在の耐震基準を満足しないものである).
ここでは,基準モデルに対して,軸応力σ0,主鉄筋比(引張鉄筋比)p1,帯鉄筋ρsをパラメータとして追加し,合計72ケースのパラメトリックシミュレーションを実施し,図3と図4に図化した.
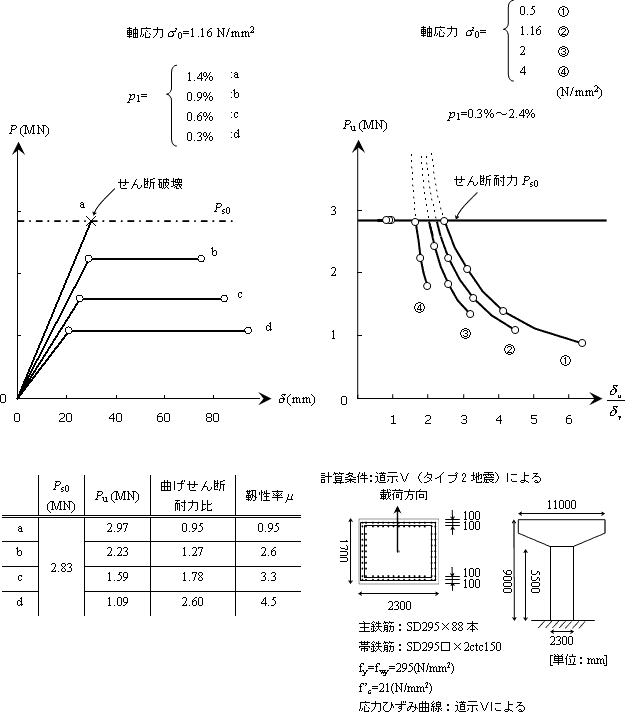 |
図3 既設橋脚(道路橋T型単柱橋脚)のP〜δ 関係と最大耐力/保有靭性 |
- 図3/左図:橋脚の荷重〜変形関係(主鉄筋p1をパラメータ)
主鉄筋p1の増大とともに,初期剛性と耐荷力は上昇する.降伏時変位δyは若干増加するが,最大変位はδu減少し,従って変位靭性率μ(=δy/δu)減少する.また,過大な主鉄筋の場合(ケースa)ではせん断破壊となり,靭性率は1を下回る(これらの数値結果は,左下の表に示している).
- 図3/右図:部材靭性率μと最大荷重Puとの関係(軸応力σ0をパラメータ):
主鉄筋p1の大小により,最大耐力が大きいと靭性率は減少,最大耐力が小さいと靭性率は増加する(これは‘低耐力高靭性/高耐力低靭性’を数値シミュレーションにて,再現したものである).
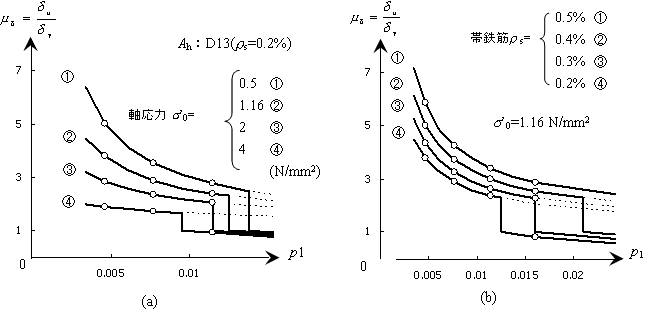 |
図4 既設橋脚(道路橋T型単柱橋脚)の保有靭性に関するシミュ−レション |
さらに,鉄筋比と靭性率の関係を図4に整理した.
- 図4右図:保有靭性率μと主鉄筋比p1との関係(軸応力σ0をパラメータ)
主鉄筋p1の増大とともに,靭性率μ(=δy/δu)は減少し,ある時点から,せん断破壊となり,靭性率は1を下回る.また,軸応力の増大は,靭性率の低下と早期のせん断破壊を招くことになる.
- 図4右図:保有靭性率μと主鉄筋比p1との関係(帯鉄筋ρsをパラメータ):
主鉄筋p1の増大により,靭性率μが減少する.主鉄筋の増大は,靭性率の低下と早期のせん断破壊に繋がる.
両図とも,軸方向筋または軸応力の増加とともに,靭性率は減少することを定量的に読み取ることができ,また,どのような場合もせん断耐力Psoを超えることはない.
上記の考察は,これまでの耐震性能評価における知見とほぼ合致するもので,本例により具体的/数値的に理解できたと言える.なお,先述のとおり,基準モデルの橋脚は,兵庫県南部地震による示方書改定前の旧示方書に準拠するもので,例えば,基部での帯鉄筋はかなり貧弱(D13ctc150mm(内外ダブル配筋),帯鉄筋体積比ρs=0.2%)であり,耐震性は低いことを付記する. |
4. 部材靭性率と応答靭性率
さて,このようにして得られた部材靭性率は,外的作用(地震動)から定まる応答塑性率と対比され,耐震設計がなされる.いわゆる,変位法による耐震設計(displacement-based
seismic design)として,基本的考え方を付記したい.
ここで,まずは,この2つの用語の定義を再確認する.
・部材靭性率:その部材が崩壊するときの終局変位.部材の最大変形能力.
・応答塑性率:ある地震荷重による応答変位.通例,最大変位を考える.
これらは,部材降伏変位にて除し,正規化して用いる(ここでは,概念と手順を示すもので,記号は敢えて用いない).
・部材靭性率=終局変位/降伏変位
・応答塑性率=最大応答変位/降伏変位
上記2量はいずれも1以上の数値であり,部材靭性率= ductility capacity,応答塑性率=
ductility demand,のように呼称/対比させると理解しやすい.
そして,最終的に耐震性照査では,次式によって判定される.
・応答塑性率<部材靭性率:OK 安全,崩壊しない
・応答塑性率>部材靭性率:NG 危険,崩壊する
以上は,変位法による耐震設計(靭性設計)の基本的な流れを示したものであるが,破壊モードが曲げ破壊(せん断破壊が回避される),構造細目が満足されている,ことなどを前提としていることは,言わずもがなである.
【参考文献】
[1] 鉄道総合技術研究所編:鉄道構造物等設計標準・同解説 コンクリート構造物,平成16年4月,丸善
[2] 日本道路協会:既設道路橋の耐震補強に関する参考資料,2 鉄筋コンクリート橋脚の耐震補強例,平成9年8月 |








