WebLesson:#4
柱部材の変形特性:P-δ曲線
-耐震性能の基本情報の見方と考え方- |
はじめに
部材の変形挙動は,荷重-変位関係(P-δ曲線とも呼ばれる)によって明快に表され,耐震性能を評価する際の基本情報となる。耐震関連の工学書/実験報告書/設計計算書では,各種各様の荷重-変形関係が提示される。優れたエンジニアは,この荷重-変形関係を見て,直ちにその構造特性/耐震性能を判断することができる。
ここでは,柱部材の荷重-変形関係の見方と考え方を理解することから始まる。荷重-変形関係の曲線上には,いくつかの重要な特異点(ひび割れ,降伏etc.)があり,これらを察知することがポイントなる。最後にRC橋脚の数値解析事例を示し,P-δ曲線の勘所を鍛錬してもらいたい。
なお,耐震工学/構造工学の分野では,(単調)荷重-変形関係,P-δ曲線,包絡線,骨格曲線,push-over解析のような表現があり,それぞれの語義・語源を持つ.ここでは,細かい定義はさて置いて,これらが結果的にほぼ同義語であるとして用いることにする。 |
1. 荷重-変位関係(P-δ曲線)の見方/考え方
荷重-変形関係を知れば(見れば),その構造部材のだいたいの構造特性/耐震性能を判断することができるが,実地震波のもとでは不規則な正負繰返し挙動となるので,まずはその包絡線を観察することが重要である。そこで,荷重-変形関係の見方/読み方を図1の3例から考えてみよう。
 |
|
 |
(a) 変位制御型繰返し静的載荷実験 |
 |
|
 |
(b) ランダム波による弾塑性動的応答解析 |
(c) 荷重−変形関係のモデル化 |
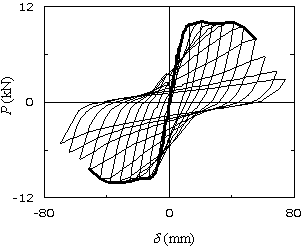
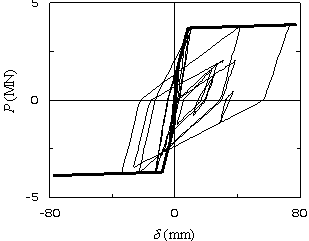
図1は,単柱形式の柱部材を片持ち梁としてモデル化した部材の力学挙動を示したものである。図1(a)
は,変位制御型正負繰返し静的載荷実験(小型試験体による実際の試験結果)である.柱部材の柱頭に繰返し変位を付与したとき(変位制御実験)の水平荷重を測定し,両者の関係を図化した。図1(b)
は,ランダム波が入力したときの動的応答変位と慣性力との関係(数値解析)を図化したもので,ランダム波のもと不規則な繰返し挙動を呈するが,正側/負側に同様の骨格曲線を有することがわかる。縦軸について,図(a)の静的荷重,図(b)の慣性力のように異なるが,ほぼ同義と考えてよい。まずは,両者の類似点と相違点を読取ってもらいたい。
ここで,図1(a)から各繰返しループのピーク点を連ねた包絡線(envelope curve),および,図(b)の骨格曲線(skeleton
curve)を太線に示し,これを3直線近似にてモデル化して,図(c)に再図化した。図(a)の包絡線は実験結果,図(b)の骨格曲線は弾塑性動的応答解析のための入力条件,との差違はあるが,両者は同様の力学的意味を持ち,いずれも荷重-変形関係(P-δ曲線)として,構造特性/耐震性能が反映された基本特性となる。このような単調な荷重-変形関係を得ることを,push-over解析(訳せば,1方向単調押切り解析)と呼ぶ。
さて,図(a)と(b)を再度比較(縦軸Pのスケール)してもらいたい。前者は,断面/320mm×320mm,高さ/1200mmの小型試験体であり,後者は,断面/D=2.7m,高さ/10mの道路橋脚であり,構造寸法が全く異なる。図(a)ではkNの単位であり,図(b)ではMNのようになっており,500倍程度の違いがあることを付記する。 |
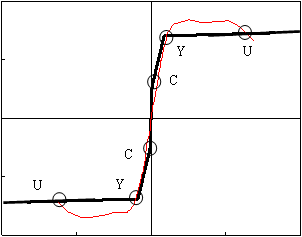
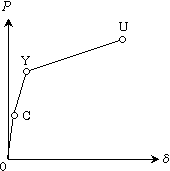
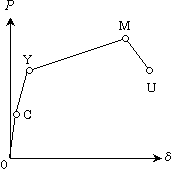
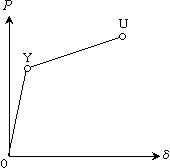
2. P-δ曲線上の特異点:C, Y, U点
荷重-変形関係の非線形特性で大切なことは,いくつかの折れ点(特異点)にて特徴付けられていることで,これらを図1(c)に併記している。最初の折れ点はひび割れ(C点)によるもので,その後のひび割れ進展とコンクリートの非線形により部材剛性が低下して,やがて引張鉄筋(軸方向筋)の降伏(Y点)により大きな折れ点を呈する。その後,荷重最大点(ピーク点)を示した後,軟化挙動を呈し,やがて終局(U点)を迎える。
これらをまとめると,
・C:crack 初期ひび割れ
・Y:yield 引張鉄筋(軸方向筋)の降伏
・U:ultimate 終局状態
初期ひび割れC点については,強地震動を考える場合あまり重要ではなく,軸方向筋の降伏点(Y点)が大きな折れ点となり,これを契機として部材剛性は著しく低下する。このY点以降,荷重の上昇は望めず,‘曲線が寝てくる’のように表現する。荷重が増大しなくても,その荷重を保持したまま変形が持続することにより靭性が確保される(耐震性が確保される)。
 |
|
 |
|
 |
(a) Tri-linear型
0→crack→yield→ultimate |
|
(b) Tetra-linear型
0→crack→yield→maximum→ultimate |
|
(c) Bi-linear型
0→yield→ultimate |
図2 多直線モデルによるP-δ曲線のモデル化 |
このような多直線モデルは分かりやすく,多くの設計/解析に用いられ,典型的な3例を図2に示した(先述の図1(c)は3直線モデルである)。これらは,応答解析における非線形挙動の包絡線となるもので,この場合は,‘骨格曲線(skeleton
curve)’と呼んだ方が適切であろう。後述する図4(b)は,道路橋示方書(V耐震設計編)に準拠した2直線モデル(bi-linear)である. |
3. 変形特性のまとめ:破壊モードと靭性
今度は,変形特性(荷重-変位関係/P-δ曲線)を,破壊モードと耐力/靭性の観点から整理してみよう。この場合,合理的かつ明快な破壊モードの階層化(hierarchical
consideration)が必要であるが,ここでは,RC橋脚を例にとりあげ,P-δ曲線を図3のように描いた。
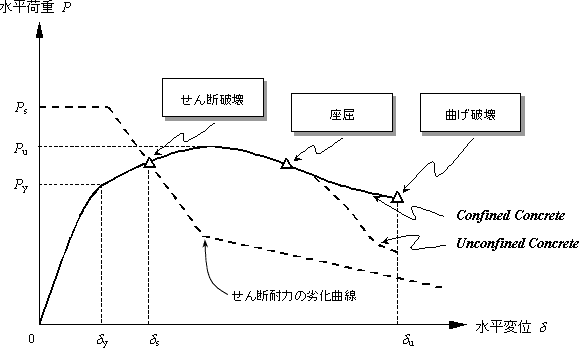 |
図3 柱部材のP-δ曲線:破壊モードと耐力/靭性からの見方 |
図3では,次のような3つ基本破壊モードに分類することにする。
・ 曲げ破壊 :設計上想定した正常な終局状態。十分靭性が確保される
・ せん断破壊:設計上回避すべき終局状態。十分な靭性が得られない
・ 局所破壊 :設計細目により防止する破壊。早期破壊となり,場合によっては十分な靭性が得られない
先述の図1の3つの変形特性はいずれも曲げ破壊であり,言わば,‘望ましい正常な部材の一生’として例示したものである。一方,せん断耐力が曲げ耐力を下回るとせん断破壊となる。図中の点線がせん断耐力を表しており,これがP-δ曲線と交差する時点にてせん断破壊となる。言い換えると,点線(せん断耐力の劣化曲線)がP-δ曲線の上方に推移すれば,設計に意図した曲げ破壊となる。
さらには,不十分な設計/構造細目により,軸方向筋の座屈,定着不良,鉄筋の疲労破断などの‘アクシデント’が発生することがあり,部材はその時点にて終局または崩壊となる。これらを局所破壊と呼ぶことにし,適切な構造設計と構造細目により防止しなければならない.例えば, 帯補強筋(せん断補強筋)の不足による早期のせん断破壊,または,主鉄筋の座屈や構造細目の不備(例えば,不適切な段落とし)により,意図された終末が達成されない場合は,所定の靭性が得られない。このことは,靭性(ductile)と脆性(brittle)によって区別されるが,十分な靭性(変形性能)が得られない場合を早期破壊(premature
failure)と呼ぶとわかりやすい。
図3はこれらのことを模式的に図化したものであり,破壊モードの制御(failure
mode control)の観点から明快な解釈を与えてくれる。ただし,同図中の‘テンコ盛りの特定点’は,一つの柱部材ですべてが観察されることはなく,例えば,せん断破壊が発生すれば部材の耐荷能力は喪失し,それ以降の変形挙動は見られない。 |
4. 数値解析例
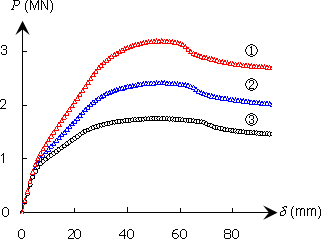
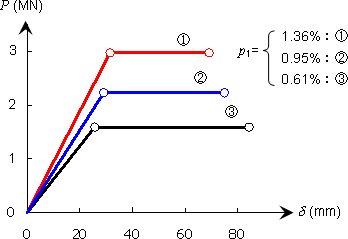
次に,荷重-変位関係(P-δ曲線)を実際に計算/図化して,その特徴を考えたい.鉄筋コンクリート橋脚の単調荷重-変形関係を数値解析し図4にまとめた(push-over解析).図(a)はファイバーモデルによる静的非線形解析であり,図(b)は,道路橋示方書(V耐震設計編)に準拠して算定したものである(いずれも,引張鉄筋比p1をパラメメータとして3曲線を併記した).
ファイバーモデル(図(a))は,材料の非線形性(ひび割れの発生と進展,鉄筋降伏)が直接反映され,曲線状を呈するが,道路橋示方書の場合(図(b)),2直線モデル(Bi-linear型)に簡略化されている.さらには,同一鉄筋比にて,ファイバーモデルと道路橋示方書とを重ね合わせると,図(c)が得られる.両手法は,3例ともに良く合致している(道路橋示方書では降伏剛性を初期剛性としているため,ファイバーモデルの方が初期の膨らみが大きく,また鉄筋降伏後の上昇が見られる).
当然のことながら,ファイバーモデルの方が実現象を良く表しており,実験結果とも合致する.道路橋示方書の場合,計算が簡略されるが,本質的な特性をわかりやすく判断できる.また,ファイバーモデルを用いる場合,専用の非線形プログラムを必要とし,道路橋示方書に準拠する場合,単純なRC橋脚であれば,電卓またはエクセルでも対処可能であることも,両者の差異である.
構造解析/耐震設計に際しての両手法の採用には,その目的に応じて使い分けることが重要である.
 |
|
 |
(a) ファイバーモデルによる解析 |
|
(b) 道路橋示方書 V耐震設計編 |
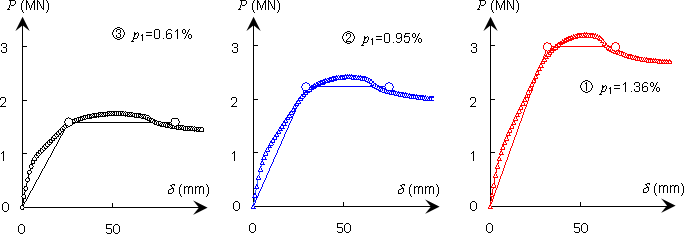
(c) 両手法の比較 |
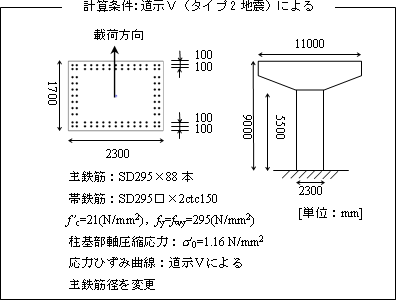
図4 曲げ破壊を対象とした荷重-変位関係:事例解析による2手法の比較 |
|
あとがき
鉄筋コンクリートの構成材料は,鉄筋では降伏と座屈,破断,コンクリートではひび割れと圧縮破壊など,特有の材料非線形(material
nonlinearity)を有する.これらを源泉として,構造部材は,部材形式/構造形式ごとに異なる非線形挙動(structural
nonlinearity)を呈する。地震時に負荷される正負の繰返し挙動により,さらに複雑な変形挙動となる.ここでは,このような複雑な挙動と破壊モードを,荷重-変位関係および線上の特異点にて理解/考察するものである。
構造部材の靭性確保から,せん断破壊,局所破壊が生じることなく,所定の位置に塑性ヒンジが形成され,曲げ破壊により終末となることが基本である。耐震性のある構造部材とは,万一,予想を越える過大な荷重が作用しても(想定した設計荷重を超えても),最終的に曲げ破壊によって一生を閉じることが保証されていることである。荷重-変位関係(P-δ曲線)は,このことを端的に表している。 |








