WebLesson:#3
軸力と曲げモーメントを受ける部材 |
はじめに
軸力と曲げモーメントを受ける鉄筋コンクリート部材の力学挙動を考える。まず,軸力作用下(通例圧縮軸力)における曲げ部材の変形挙動(M-φ関係)を概観する。終局耐力の算定式(塑性解析:等価矩形応力ブロック法)を提示し,軸力と曲げの相互作用図について説明する。
軸力と曲げモーメントを受ける断面の終局耐力は,M-N破壊包絡線(M-N failure
envelope)によって記述され,これは2つの断面力がお互いに影響を与えることから,M-N相互作用図(M-N
interaction curve)ともよばれる。併せて,断面の曲率と靭性率にも考察し,これは鉄筋コンクリート橋脚の耐震性能の評価にきわめて重要となる。 |
1. 軸力と曲げモーメントを受けるときの非線形挙動
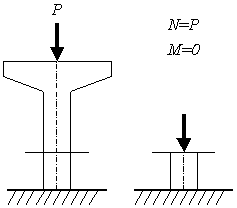
図1のような,鉛直荷重Pを受ける単柱形式の柱部材を例にとり,作用する2つの断面力(N’=軸力,M=曲げモーメント)を考える。
 |
|
 |
| (1)中心軸圧縮力 |
|
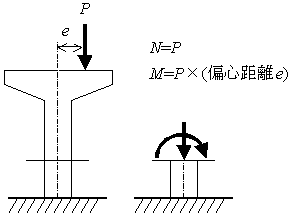
(2)偏心軸圧縮力 |
図1 軸力と曲げモーメントを受ける部材の考え方:中心/偏心軸圧縮状態 |
これは,以下のように分類できる。
(1) 中心軸圧縮状態:断面には,軸力(圧縮)のみが作用
(2) 偏心軸圧縮状態:断面には,軸力と曲げモーメントが作用
ここでeは断面図心からの偏心距離を表し,e=M / Nにより定義されるが, M =
e×Nのように考えてよい。
次に,軸力N’をパラメータとした変形挙動と終局時の特性を,図2のようにまとめた。これは,
(a) M-φ関係
(b) 軸力N’-終局曲げ耐力Mu関係
(c) 軸力N’-終局曲率φu関係
の3図を関連させて示したものである。パラメータとした軸力(圧縮のみを考える)は,小さい方から,(1)〜(4)のように付番した。特に,(1)N’=0,(2)一般的な橋脚の作用軸力,(3)釣合い破壊(後述にて説明),(4)軸圧縮破壊の70%程度,としていることに留意されたい。
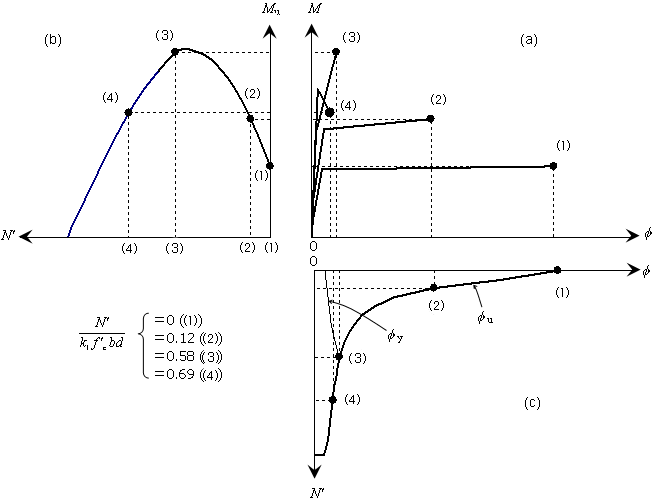 |
| 図2 (a) M-φ関係,(b) 軸力N’-終局曲げ耐力Mu関係,(c) 軸力N’-終局曲率φu関係 |
図2から,軸力レベル(3)を境に,次のような特徴が読み取れる。
・軸力レベル(1)〜(3):軸力N’が増加すると,M-φ関係は上昇し,最大耐力Muは増加するが,一方では,終局時の曲率φuは減少する。
・軸力レベル(3)〜(4):軸力N’の増加により最大耐力Muおよび終局曲率φuがともに減少する。このことは,図(b) N’-Mu関係,図(c) N’-φuにおいて,Muおよびφuを軸力N’の関数として見ると容易に判断できる。
・軸力N’の増加に伴い,最大耐力Muは(3)釣合い破壊点にてピークを有するのに対して,終局曲率φuは単調減少となる。
ここで,軸力レベル(3)は釣合い破壊時の軸力を用いたもので,これを境として,
・軸力レベル(1)〜(3) (N’≦N’b) ⇒ 鉄筋降伏先行型
・軸力レベル(3)〜(4) (N’≧N’b) ⇒ コンクリート圧縮破壊型
のように,破壊形式を分類できる。また,軸力をさらに増大して軸力のみで破壊した状態が,単軸挙動となる。 |
2. 終局耐力の算定方法
ここで,断面の終局耐力をMu,N’uのように表示し,その算定法を提示するため,図3のような断面仮定(複鉄筋長方形断面を考える)と記号を用いる。その算出法は以下のようにまとめられる。
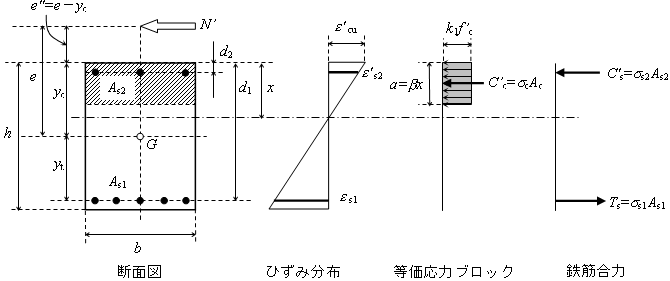 |
図3 終局耐力の算定に関する断面仮定と記号 |
(1)偏心量eに対する終局耐力を求めるが,軸方向力と曲げモーメントの釣合いが基本式となる。
(2)ひずみ分布は断面内で線形分布と仮定し,コンクリートの応力については引張側を無視し,圧縮側は等価矩形応力ブロックを採用する。
(3)圧縮/引張鉄筋については,弾性状態(降伏前)か降伏後を判定する必要がある。
(4)断面の終局状態は,「コンクリートの圧縮縁ひずみがその限界値ε’cuに達したとき」により定義される。
ここで,土木学会コンクリート標準示方書[2]では,具体的な数値として次式を与えている(コンクリートの圧縮強度をf’cとしている)。
| ・終局ひずみ : |
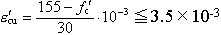 |
| ・等価応力ブロックの3係数 : |
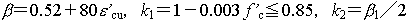 |
上記は,高強度コンクリートを含めた現行示方書の規定値であるが,普通コンクリートの場合,旧示方書[3]の値が簡便であり,概略値として覚えておくとよい。
| ・等価応力ブロックの3係数 : |
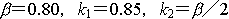 |
| ・終局ひずみ : |
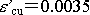 |
このような仮定のもとに断面の終局耐力Mu,N’uに関する釣合い式は,以下のように整理することができる。
|
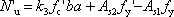 |
(1) |
|
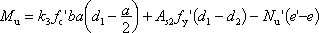 |
(2) |
また,断面耐力に無次元表示 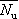 , , 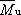 を用いると,次式のようにも記述できる。 を用いると,次式のようにも記述できる。
|
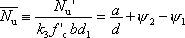 |
(3) |
|
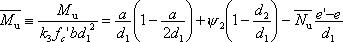 |
(4) |
ここで、
|
偏心量 : |
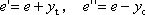 |
|
|
鉄筋係数: |
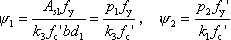 |
(5) |
(読者は,式(3)〜(5)がそれぞれ無次元になっていることを確認されたい)。
以上の算定式右辺のうち,コンクリート応力ブロック高さα (図3参照)のみが未知数であり,これは,それぞれの破壊形式に対して,以下のように与えられる。ただし,γ=d2/d1としている。
|
・釣合い偏心状態の場合(添え字 b を付している):
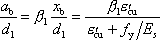 |
(6) |
|
・鉄筋降伏先行型(N’≦N’b,e≧eb)の場合:
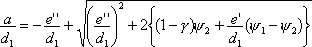 |
(7) |
|
・コンクリート圧縮破壊型(N’>N’b,e<eb)の場合:
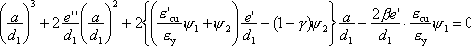 |
(8) |
ここで,圧縮/引張鉄筋の応力が,未降伏(弾性状態)の場合,作用している鉄筋応力を算出して,これを降伏強度の替わりに用いる必要があり,詳しくは関連文献(例えば,[4])を参照されたい。
|
3. Mu-N’u曲線:破壊包絡線(相互作用図)
3.1 断面のひずみ分布
偏心量をe=0から始まるパラメータとして考え,断面のひずみ分布を描くと,図4のように図示できる。偏心量e=0の状態は中心軸圧縮力を受ける時を表し,e=∞の状態は曲げのみを受ける状態に相当する。
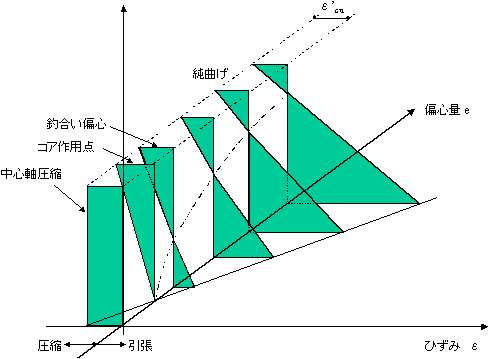 |
図4 種々の偏心量eにおける断面のひずみ分布 |
ここで,釣合い破壊時およびこれによって分類される2つの破壊形式に対して,引張鉄筋のひずみεs1とコンクリートの圧縮縁ひずみε'cを,次のように整理できるので図4と関連して確認されたい。ここで大切なことは,いずれの場合も,コンクリートの圧縮縁に対して,ε’c=ε’cuなる条件にて終局と定義されていることである。
| ・鉄筋降伏先行型(N’≦N’b,e≧eb) |
→ 両材料のひずみ:εs1≧εy,ε’c=ε’cu |
| ・釣合い破壊時(N’=N’b,e=eb) |
→ 両材料のひずみ:εs1=εy,ε’c=ε’cu |
| ・コンクリート圧縮破壊型(N’>N’b,e<eb) |
→ 両材料のひずみ:εs1<εy,ε’c=ε’cu |
なお,両材料の限界ひずみは,引張鉄筋に対してεy=fy/Es,圧縮コンクリートに対してε’cu=(155−f’c)/30×10-3(前出)のように与えられる。 |
3.2破壊包絡線/相互作用図の見方
以上の考察をもとに,偏心量eをパラメータとして終局耐力Mu,N’uを算出すると,図5のような相互作用図(interaction curve)を作画することができる。これは,破壊包絡線(failure
envelope)と呼ぶこともある。
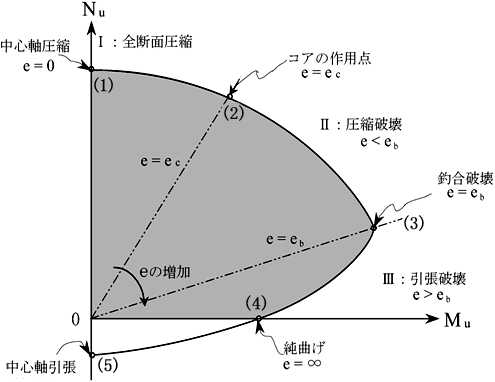 |
図5 Mu,N’uに関する相互作用図(破壊包絡線) |
図5の相互作用図では,まず,図中に記した(1),(2),(3),(4),(5)の主要点を理解することがポイントである。すなわち,e=0から出発して,順に下記のように定義できる。
(1)単軸圧縮破壊(e=0)
(2)コア作用点(e=ec)
(3)釣合い破壊(e=eb)
(4)純曲げ破壊(e=∞)
(5)単軸引張破壊
(3)釣合い破壊(e=eb)を遷移点として,2つの破壊形式に分類できることは,前述のとおりで,これは次のように整理できる。
・鉄筋降伏先行型(N’≦N’b,e≧eb):曲げモーメントの増大に伴い,引張ひび割れの発生/進展,中立軸の上昇,引張鉄筋の降伏,圧縮コンクリートの圧縮破壊,と典型的な非線形挙動を観察することができる。これは軸力のレベルが小さいので,純曲げの場合と同様な挙動を示す。破壊の様相も穏やかであり,比較的靭性に富むことは,図2にて説明したとおりである。
・コンクリート圧縮破壊型(N’>N’b,e<eb):曲げモーメントの増大に伴い引張ひび割れは発生するが,ほとんど進展がなく,引張鉄筋が未降伏のまま,コンクリートの圧縮破壊を迎える。これは,ひずみ分布(図4)から判断されるように,中立軸が図心軸より下方にあり,引張鉄筋の負荷が小さいことによる。終局時には,明瞭な予兆のない脆性的な破壊となり,急激な耐力低下を呈する。このような特性は,(引張鉄筋未降伏のため,脆性的に破壊するという意味で)純曲げ状態の過鉄筋(over-reinforcement)と同じではあるが,純曲げの場合,設計上(配筋上)回避されなければならないのに対して,過鉄筋でない断面(under-reinforcement)であっても,軸力が加わることにより,釣合い破壊およびコンクリート圧縮破壊型はその包絡線上に必ず存在する。 |
4. 降伏/終局時の曲率と曲率靭性率:N’u-Mu-φu曲線
今度は,相互作用図に,降伏時および終局時の曲率を加えると,図6のようにまとめることができ,ここでも軸力をパラメータとして考える。曲げ部材の曲率φは,平面保持の仮定が成立している断面のひずみ分布の勾配をあらわすもので,軸ひずみが,ε(y)=ε0+φ・yのように与えられることは,弾性問題にて学習したとおりである。曲率φの次元は[1/長さ]となり,例えば,1/mが用いられるが,無次元量として,φdのようにすることが多い。鉄筋コンクリート断面の場合,中立軸の位置をxとして,下式のいずれかにて算定される(図3の断面記号を用いている)。
|
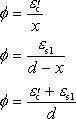 |
(9) |
降伏時の曲率φyはεs1=εyとして,および,終局時の曲率φuはε’c=ε’cuとして,上式に従い求めることができる。ただし,実際の算定に際しては,中立軸位置と引張/圧縮鉄筋の降伏判定など,複鉄筋長方形断面に限定しても解析解を得ることは容易ではない。そこで,断面を層状に離散化したファイバーモデルが用いられることが多い。
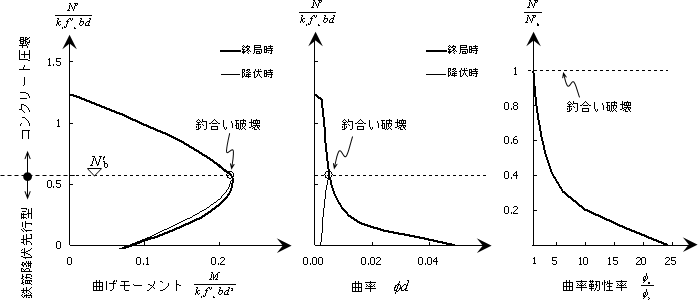 |
図6 (a)M-N破壊包絡線, (b)降伏曲率φy,終局曲率φu,(c)曲率靭性率μφ |
また,図6(a),(b)では,降伏時を細線,終局時を太線にて表しているが,断面耐力(降伏モーメントMy,終局耐力Mu)を含めて考えると,RC断面の力学的特性をよく表していると言える(これは,鉄筋降伏先行型(N’≦N’b,e≧eb)に限定されるが)。すなわち,軸力の増大とともに(N’=0→N’b),断面耐力My,Muはともに増加するが,MyからMuの伸びがほとんどない(側方鉄筋の鉄筋量にも関係する)のに対して,降伏曲率φyは増加,終局曲率φuは減少していることがわかる。
ここで,両者の比をとり,断面の曲率靭性率をμφ=φu/φyのように定義する。曲率靭性率(curvature ductility)は,曲げモーメントを受ける断面の降伏から終局までの変形(曲率)の伸びを示すもので,断面の靭性を端的に表すものである。図6(c)に図示したように,軸力の増加とともに曲率靭性率μφは減少し,釣合い破壊点にて1となり,これを超える大きな軸力の作用下では,靭性が期待できないことになる。 |
【参考文献】
[2] 土木学会コンクリート委員会:2002年制定コンクリート標準示方書[構造性能照査編]
[3] 土木学会コンクリート委員会:コンクリート標準示方書[平成3年版]設計編
[4] 吉川弘道:第2版 鉄筋コンクリートの解析と設計-限界状態設計法と性能設計法-,第5章,one
pointアドバイス#7,p.121,丸善,平成16年2月 |
あとがき
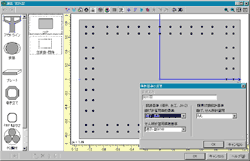
本講における数値シミュレーションには,汎用の断面計算プログラムUC-win/Section(株式会社フォーラムエイト)を用いている。様々な断面形状,ならびに2軸曲げ作用状態の耐力・応力の評価が可能で,実務設計から教育用途まで幅広く利用できる。以下は,実行画面の例である。
 |
 |
| (a) 断面の作成と準拠基準の選択 |
(b) 応力・ひずみ分布確認画面 |
 |
 |
| (c) 水平軸回りのM-φ曲線 |
(d) M(My,Mu)-N相互作用図 |
図 UC-win/ Section による実行画面 |
|








