WebLesson:#12
高橋脚を有する連続桁橋の幾何学的非線形解析
株式会社 フォーラムエイト 技術サポートグループ |
はじめに
主に山岳部に構築されることが多い高橋脚では,一般に地震時の水平変位が大きくなる.橋脚天端の変位増大に伴い,上部構造からの死荷重が柱基部に対して偏心し,その付加モーメントの影響が懸念される.
本例では,高さが約40mの高橋脚に対して,幾何学的非線形を考慮した時刻歴応答解析を行い,微小変位理論解析結果との比較を行うことにより,幾何学的非線形性の影響を考察した. |

(株)大林組(http://www.obayashi.co.jp/)より
上記写真は本検討とは一切関係ございません
|
1. 対象橋梁/解析モデル/材料モデル
対象橋梁:
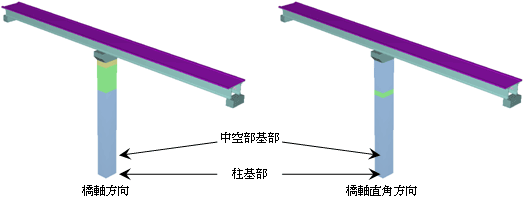
本例での対象構造物は,下図のように橋長約90mの二径間連続桁橋とし、両端のA1、A2橋台と中間橋脚にて支持されている.中間橋脚の高さは約40mである.
支承条件は固定/可動支承であり,A1橋台のみ固定である.橋脚の柱基部から4.0mまでは充実断面であり,それより上部では中空断面となっている.
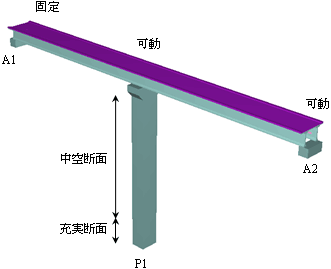 |
| 図1. 解析対象構造物の構造物概要 |
|
解析モデル:
解析モデルは下図のような骨組みモデルとする.上部構造と橋台は弾性部材とし,非線形部材は橋脚柱部のみにファイバー要素を用いる.支承はバネ要素でモデル化する.
地盤種別はI種地盤,A地域とする.入力する加速度波形は,道路橋示方書巻末資料のII-I-1とし,橋軸方向および橋軸直角方向に入力する.
なお,本解析はUC-win/FRAME(3D) Ver.3.00.03を用いて行う.
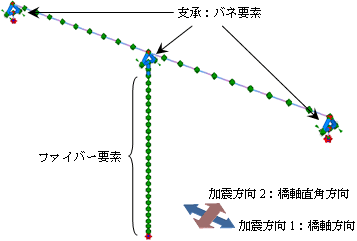 |
| 図2.解析モデル |
|
材料モデル:
ファイバー要素のヒステリシスはコアコンクリート,かぶりコンクリート,鉄筋の3要素に対して下図のように定義する.
 |
|
 |
|
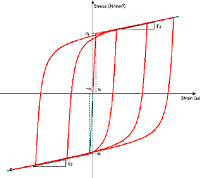 |
| かぶりコンクリート |
|
コアコンクリート |
|
鉄筋 |
図3.ヒステリシス |
|
入力地震動:
減衰は要素別剛性比例型とし,弾性域のコンクリートは4%,ファイバー要素でモデル化した部材については0%として履歴減衰のみ考慮することとする.
入力する加速度波形は道示波II-I-1(図4)とする.
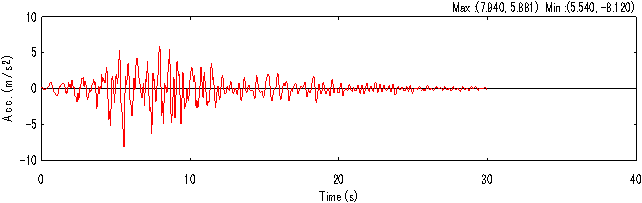 |
図4.加速度波形 |
|
2. 解析結果(微小変位)
まずは,通例の微小変位理論に基づいた時刻歴応答解析を行い,その結果を以下に示す.橋軸方向は可動条件であるため橋脚基部のひずみが大きくなっている.橋軸直角方向は並進方向固定,かつ,橋軸回りの回転を拘束するため,柱頭部にも大きなひずみを記録している(ただし、鉄筋が降伏するほどではない).
 |
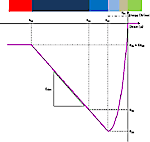 |
図5.最大ひずみ分布 |
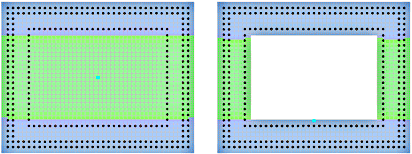 |
| (a) 橋軸方向加震の場合 |
 |
(b) 橋軸直角方向加震の場合
図6.柱基部/左図と中空部基部/右図の最大ひずみ分布 |
次に柱天端での、応答変位の履歴を示す.
橋軸方向の最大変位は約680mmを記録し大きく振動しており,橋脚高40mの1%(=400mm)を上回っていることがわかる.このとき,上部構造の重量作用位置(支承位置)は図8のように偏心状態にあり,幾何学的な影響(付加モーメント)があるものと推察できる.
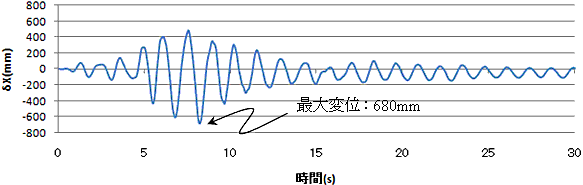 |
(a) 橋軸方向変位履歴 |
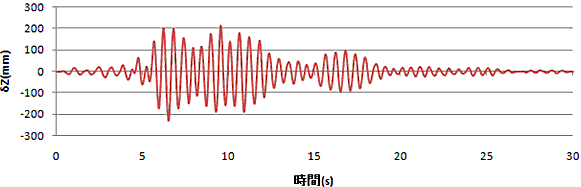 |
(b) 橋軸直角方向変位履歴
図7.橋脚天端の応答変位履歴 |
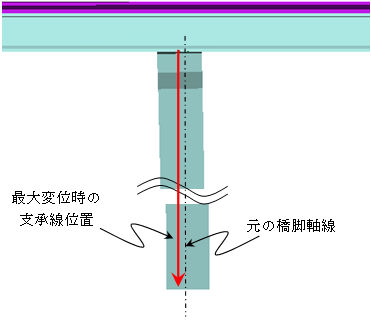 |
| 図8.最大変位時の荷重状態 |
|
3. 解析結果(大変位)
上記の検討より,橋軸方向加震では幾何学的な影響が無視できないため,大変位解析(幾何学的非線形解析)を行った.以下に微小変位解析を行った結果との比較を示す.
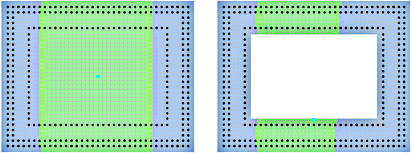
図9は両者の最大ひずみ分布である.左側の大変位解析結果の方が柱基部でより大きなひずみを示している.偏心状態になり,柱基部に付加モーメントが作用しているものと思われる.
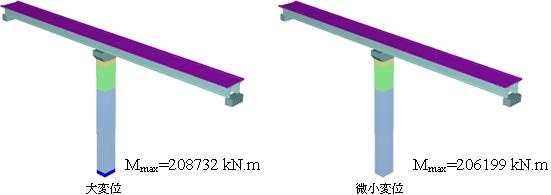 |
図9.最大ひずみ分布の比較(橋軸方向加震) |
柱基部の断面に着目すると,大変位解析結果のかぶりコンクリートの一部にポストピーク領域が認められる.
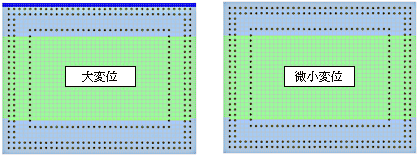 |
|
 |
| 図10.最大ひずみ分布断面図 |
橋脚天端での変位履歴を下図に示す.
大変位解析ではδmax=707mmとなり,微小変位解析のδmax=680mmに対して約4%増加している.
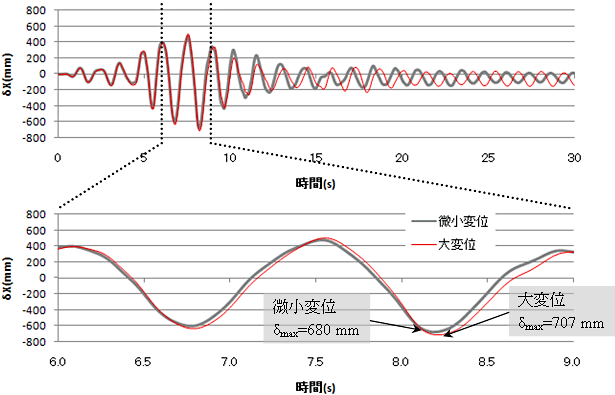 |
図11.変位履歴の比較 |
|
4. まとめ
- 橋脚高約40mの高橋脚を有する2径間連続桁橋に対して、幾何学的非線形性を考慮した時刻歴応答解析を行った.
- 微小変位解析の結果,橋脚天端での変位は最大680mmとなり,微小変位解析の範疇を超過していた.
- このため,大変位解析を行った結果,橋脚天端での変位は最大707mm(橋軸方向加震の場合)となり,本対象橋脚では幾何学的な影響は無視できないことが判明した.
参考文献
- 社団法人 日本道路協会:道路橋示方書・同解説 V耐震設計編,平成14年3月
- 東・中・西日本高速道路株式会社:設計要領第二集 橋梁建設編,平成18年4月
- 社団法人 土木学会:橋の動的耐震設計,平成15年3月
|








