| �@�R�D��͊֘A |
�p�R�|�P�D |
�ÓI��́A���I��͎��̉d�����͂ǂ̂悤�ȑg�ݍ��킹�Őv�\���H |
| �`�R�|�P�D |
�ÓI��͂̏ꍇ�Gdead+static�Astatic�̌v�Z���\�ł��B
���I��͂̏ꍇ�Gdead+static+dynamic�Adead+dynamic�Astatic+dynamic�Adynamic�̌v�Z���\�ł��B
�A���Adead���l�����Ȃ��ꍇ�A���f�����d�ɂ�鉔�����d����������邱�ƂɂȂ�܂��̂Œ��ӊ肢�܂��B
���A������1.01.00������{��v���b�g�t�H�[���ɑΉ����Ă���܂��̂ŁA�d�^�C�v�̒�`�ł�
�����d�idead�j�@���ÓI�d�istatic�j�@�����I�d�idynamic�j
�̑g�ݍ��킹�I�������Ƃʼn\�ƂȂ�܂��B |
| �@ |
|
| �p�R�|�Q�D |
�n�k�g�͍ő�U���̑O������Ηǂ����H |
| �`�R�|�Q�D |
���ۂɉ�͂ɗ��p����g�`�Ƃ��ẮA�n�k���̔g�`�S�Ă𗘗p���Ă����܂�Ӗ��͂���܂���B
���̂��Ƃ���A�ő�ƂȂ�U���g�`�����ɂ߂��̑O��𗘗p���邱�ƂŖ��͂���܂���B
�܂��A�^�C���X�e�b�v��e������Ēn�k�g�f�[�^�𗬂��ĉ����l�̕ϓ���͂�A�n�k�g�f�[�^�͈̔͂�I�肳���̂��悢�ƍl���܂��B |
| �@ |
|
| �p�R�|�R�D |
�R���N���[�g�̉��́[�Ђ��݊W���������́A�ǂ̂悤�ɂ��Ă���̂��H |
| �`�R�|�R�D |
�Ђъ��ꔭ���O�̃R���N���[�g�̍\�����͑O��E�����̒e�Y���j�f�����̗p���Ă���A
����ɂ����Ă͓������͂Ɠ����Ђ��݂̊W���莮������Ă��܂��B
�i�\�����j
�@��e = E0�EK0�E��e
�@ = E0�EK0�E(��-��p)
�@��e�F��������=( ( a�E��m )�O2 + ( b�E��d )2 )�O1/2�@�@
�@a = 0.6/fc�f , b = 1,3/fc�f , fc�f�F�ő剞�́@,�@ ��m�F���ω��� , ��d�F������
�@��e�F�����Ђ���
�@�ÁF�����S�Ђ���=( ( c�E��m )�O2 + ( d�E��d )2 )�O1/2
�@c = 0.62/��c0�f, d = 0.98/��c0�f,
�@��c0�f�F�ő刳�k���͂ɑΉ�����Ђ��� , ��m�F���ςЂ��� , ��d�F���Ђ���
�@��p�F�����Y���Ђ��݁i���͂�0�Ɛ������Ƃ��̓����Y���Ђ��݁j
�@E0 = 2, K0�F�j��p�����[�^
�������Ђ��݂�����܂łɌo�������ő�l���z���Ȃ����蓙���Y���Ђ��݂Ɣj��p�����[�^�͕ω����Ȃ��B
�@��p�F�����Y���Ђ��݁@�@K0�F�j��p�����[�^�͎������ʂɊ�Â��莮��
�@��p = c�E(1-exp(-0.35�E��))
�@K0 =�@exp(-0.73�E�ÁE(1-exp(-1.25�E��))) |
| �@ |
|
| �p�R�|�S�D |
�n�Վ�ʂɉ���������f����G0�Ƃ���f���xSu�̊W
�r�����f0/600�@ For�@clay�@�r�����f0/1100 For sand
�͂ǂ̂悤�Ɍ��߂�ꂽ�l�Ȃ̂��H |
| �`�R�|�S�D |
�_���uOhsaki, Y. : Some notes on Masing's law and nonlinear response and
soil deposits,Journal of the Faculity of Eng.(B), The University of Tokyo,
Vol.XXXV,No.4, 1980�v�̃y�[�W�T�Q�R�y�[�W�Ɉȉ��̋L�q������܂��B
"In Figs. 8 and 9, a large number of laboratory test results on strain-dependent,
shear modulus ratios for clays and sands, respectively are summarized,
and Figs 10 and 11 show the test results on damping factors which are also
strain-dependent.
On the other hand, the curves in these figures are obtained from eqs. (19)
and (23) by assuming G0/Su=600and 1100 for clays and sands, respectively.
The agreement of laboratory test results and calculated curves is excellent
over the entire level of strains fron=m approximately 0.001up to 1 per
cent."
�����A�����̎����f�[�^�Ɖ�͌��ʂ��r�����f0/600(clay)�A�y�� �f0/1100(sand)�̒l�����߂�ꂽ���̂ƕ��Ђł͗������Ă���܂��B |
| �@ |
|
| �p�R�|�T�D |
��͐͌��ʂ́uActive�N���b�N�v�Ƃ͂ǂ̂悤�ȏ�Ԃ��H |
| �`�R�|�T�D |
UC-win/WCOMD�ł́A��������2�̂Ђъ�����W�n��p���āA���v4�����̂Ђъ����\�����܂��B
����4�����̂Ђъ���̂����A�ŏ��ɐ������Ђъ���ɑ��Ă܂��Ђъ�����W�n���Œ肳��A������1�Ђъ���i���W�n�j�ƌĂт܂��B�����āA��1�Ђъ���i���W�n�j�ƈقȂ�����ɂЂт�ꂪ������ƁA����ɂ��킹�đ�2�Ђъ���i���W�n�j���Œ肳��܂��B
�@�����āA��1�Ђъ���i���W�n�j�Ƒ�2�Ђъ���i���W�n�j�������ɔ������Ă���ꍇ�A�Ђъ��ꂪ���J���Ă���Ђъ���i���W�n�j�̂��Ƃ��uActive�N���b�N�v�ƌĂ�ł��܂��B�]���āA�d�̏�Ԃɉ����A��1�Ђъ���i���W�n�j���uActive�N���b�N�v�ɂȂ�����A��2�Ђъ���i���W�n�j���uActive�N���b�N�v�ɂȂ����肷�邱�ƂɂȂ�܂��B
�@�Ȃ��A����f�ό`�́uActive�N���b�N�v�ɑ��Ă̂ݍl������܂��B��������̂Ђъ���i���W�n�j�ł���uDormant�N���b�N�v�ɑ��ẮA����f�ό`�͍l������܂���B���̃��f�����̑Ó����͐��l�������ʂ�ʂ��Č�����Ă��܂��B
�u��1�Ђъ���Ƃ����̂́ARC���ډׂ���ۂɂ͂��߂ăR���N���[�g�̎�����c���A�������E�c�i�ʏ�0.01�`0.03%�A�R���N���[�g�̉��͂��j�����ɓ��B�������̎�����c������ʓI�ɑ傫���j�ɒB�������ɔ�������Ђъ���ł��B���̊p�x�͎�������͂̍�p�����ɒ��p�ł��B����ɑ��đ�2�Ђъ���Ƃ����̂́A������͓����ł͂���܂������̕�������1�Ђъ���Ƃ̌��p��15�x�ȏ�ƂȂ�Ђъ���̎��������܂��B�v |
| �@ |
|
| �p�R�|�U�D |
�S�̔j�f�i�������x�j�ɂ��ẮA�ǂ̂悤�ɍl���Ă��邩�H |
| �`�R�|�U�D |
�S�ؔj�f�ɂ��Ă͍l�����Ă���܂���B
�{�v���O�����̍\�����ł́A�j�f�Ђ��ݑ����ȏ�̂Ђ��݂��������ꍇ���A�S�̉��͂͏㏸���Â��܂��B
�������A�A�h�o���X���[�h�ł��ő�10%�̂Ђ��݂܂ł����Ή��ł��܂���B
����́A����ȏ�̂Ђ��ݗ̈�ł́AWCOMD�̍\�����̐��x�������Ȃ鎖���l������ׁA�����Ƃ��Ă���܂��B�]���āA�j�f�Ђ��݂�10%�ȏ�ƍl����ꍇ�́A�S�̔j�f�܂Ōv�Z���s�����Ƃ͏o���܂���B |
| �@ |
|
| �p�R�|�V�D |
�v�f�̉��͓x�͉���\���Ă��邩�H |
| �`�R�|�V�D |
�v�f�̉��͓x�̕\���́ARC�v�f�Ƃ��Ẳ��͓x�i�S�ƃR���N���[�g���܂ށj��\���Ă��܂��B
�K�E�X�_�̉��͂��ЂƂ���Ɨ͂̂肠�����́A
�Ё���c�{p�E��s�@�i��c�F�R���N���[�g���́Ap�F�S�ؔ�A��s�F�S�؉��́j
�ƂȂ�܂��B
"���͓x����"�A�����"�K�E�X�_�ł̌���"�ŕ\������鉞�͂́A�㎮�̃Ђ�\�����Ă��܂��B |
| �@ |
|
| �p�R�|�W�D |
Peak Strain Damage��Considerable Damaage Criteria:��c�肷��Ђ��݂̎Z�o�����́H |
| �`�R�|�W�D |
Considerable�@Damaage�@Criteria�����߂郿�̌W���̒l�̓x�[�V�b�N���[�h�ł̓f�t�H���g�Ƃ��ă�=1.5�Ƃ��Ă���A�A�h�o���X���[�h�ł͔C�ӓ��͂��\�Ƃ��Ă��܂��B
�f�t�H���g�l�̍����́A�Ⴆ�Γy�؊w��̃R���N���[�g�W���������ɂ���R���N���[�g�̈��k���E�Ђ��݂Ȃǂ����l���������B
���̊�ł̓s�[�N���̂Ђ��݂�2000�ʁA���k���E�Ђ��݂�3500�ʂƂ��Ă��܂��B�]���āA���k���E�Ђ��݂̓�peak��1.5�{�ƂȂ�킯�ł��B
�����ň��k���x��21N/mm^2�Ƃ���ƁAHELP�h���k�s�[�N�Ђ��݁h�ɋL�ڂ̂��Ă���v�Z���ŎZ�o����ƁA��peak��2000�ʁB�]���āA���k���E�Ђ��݂�1.5�{��3500�ʂƍl���邱�Ƃ��ł��܂��B�������A��葹���̑傫����Ԃ����l���Ȃ�A��=2�Ƃ��邱�Ƃ��ł��܂��B
�d�x�̑�����Ԃ��ǂ̂悤�ȏ�ԂƑz�肷�邩�����l���̏�A�A�h�o���X���[�h�ł͓��͂��������B |
| �@ |
|
| �p�R�|�X�D |
�K�E�X�_�̂Ђ��݂ɂ��āB |
| �`�R�|�X�D |
�K�E�X�_�̂��Ђ��݂ɂ�2��ނ���܂��D
�@�@(1)�@�u�K�E�X�_�̌��ʁv���瓾����Ђ���
�@�@(2)�@�u�Ђъ��ꌋ�ʁv���瓾����Ђ���
(1)�́C�S�̍��W�n��X�CY�CXY�����̂Ђ��݂Ɖ��͐�����\���������̂ł��D
(2)�́C�Ђъ���ʂɑ��C���s�C�����C����т���̂Ђ��ݐ�����\���������̂ł��D
�]���ė��҂͊�ƂȂ���W�n���قȂ�܂��D�����C�j���̔���͇A�̂Ђ��݂ōs���܂��D
(1)�@�K�E�X�_�̌��ʂ��瓾����Ђ��݂ɂ���
�@�@�w�͂��߂Ɂx���wUC-win/WCOMD�K�C�h�x���w�K�E�X�_�ł̌��ʁx�ɐ������Ă��܂��D
�@�@�K�E�X�_�̌��ʂł́C�S�X�e�b�v�ł̕��ω��͂ƕ��ςЂ��݂̊W��xx-��xx�C��syy-��yy�C��xy-��xy���m�F���邱�Ƃ��ł��܂��D
(2)�@�Ђъ��ꌋ�ʂ��瓾����Ђ��݂ɂ���
�@�@�w�͂��߂Ɂx���wUC-win/WCOMD�K�C�h�x���w�Ђт��i�J���j���ʁC�Ђъ���i����j���ʁx�ɐ������Ă��܂��D
�@�@�K�E�X�_�̂Ђъ��ꌋ�ʁi�����Ђ��݁A���k�Ђ��݁A����f�Ђ��݁j�́C�v�f���ɁC�܂����ڂ�������X�e�b�v�ł̒l�����o�͂��邱�Ƃ��o���܂���D
�@�@�u�Ђъ��ꌋ�ʁv->�u���ڃX�e�b�v�w��v���s���C�����āu�v�f�N���b�N�v->�u���l��Y�t�v�ƍs���C���ʂ�HTML�t�@�C�����ɏo�͂ł��܂��D
�܂��C�K�E�X�_�̂Ђ��݂̌��ʂ͏o�͌`�Ԃɂ��킹�ȉ��̂悤�ɕ��ނł��܂��D���Q�l�ɂ��Ă��������D
���I�������v�f�̂���X�e�b�v�ł̏���\���C�o�͂������
�@�������ʁi�c���j
�@�������ʁi�ő�j
�@�Ђъ���i�J���j����
�@�Ђъ���i����j����
�@���͓x����
�@�~������
���S�X�e�b�v�̏���\���C�o�͂������
�@�K�E�X�_�ł̌��� |
| �@ |
|
| �p�R�|�P�O�D |
�d�x�����̓w���v�ŃR���N���[�g�̔j��̕�C�^�C���ɑ��ė��p�����Ə����Ă������A�d�v�����x�̊�̓��~��peak�Ƃ����̂ŁA�R���N���[�g�̈����ɑ�����̂��i�����Ƃ���f�j����j�B |
| �`�R�|�P�O�D |
�d�x�̑����̓R���N���[�g�̈��k�Ђ��݂݂̂Ŕ��肵�Ă���A���k�����̒��x��]�����Ă��邱�ƂɂȂ�܂��B�����ɂ�鑹���ɂ��ẮA�y���ȑ����݂̂肵�Ă��܂��B
�ʏ�̐v�ΏۂƂȂ镔�ނ́A����f�j�邩���Ȃ����A�����āA���Ȃ��ꍇ�ɂ͈��k�͂ɂ�鑹�����ǂ̒��x���]�����邱�Ƃ��d�v�ƍl���Ă���܂��̂ŁA����f�����̒��x�͕]���̑ΏۂƂ��Ă��܂���B�܂��A�����Ɣj���̍l�����ɂ��Ĉȉ��ɉ�������Ă��������܂����̂ŎQ�l�ɂ��Ă��������B
���y���ȑ����E�E�E�Ђъ��꒼������̃R���N���[�g�����Ђ��݂���t�ȏ�
�@��{���[�h�ł͐����l�i0.1%)���ݒ肳��Ă��܂��B
�@�y�؊w��̂Ђъ��ꕝ�Z�莮�Ƌ��e�Ђъ��ꕝ�����狁�߂邱�Ƃ��ł��܂��B�]���āA�g�p���E��Ԃ̏ƍ��Ɏg�p���邱�Ƃ��o���܂��B
���d�x�̑����E�E�E�R���N���[�g���k�Ђ��݂����~�Áfpeak�ȏ�
�@�R���N���[�g�̈��k�����̒��x��\���Ă��܂��B�@��ʂɁA�R���N���[�g���k�s�[�N�Ђ��݁F�Áfpeak=0.2%���x�A�R���N���[�g�I�Lj��k�Ђ��݁F�Áfcu=0.2%�`0.5%���x�ł��邱�Ƃ���A��=�Áfcu/�Áfpeak=1.0�`3.0���x�ƍl���Ă܂��B��{���[�h�ł͐����l�i��=1.5)���ݒ肳��Ă��܂��B
�@���y���E�d�x�A�����̑������o�������v�f�́A�ő呹���̕\���ɂ����ďd�x�̑������\������܂��B
���j��
�@������Ƃ͑S���ʂɒ�߂���̂ŁA���k�j��A�����j��A����f�j��A���ꂼ��̔j�����Ђ��݂Œ�`���܂��B�����̗L���ɊW�Ȃ��K�p����܂��B�x�[�V�b�N���[�h�ł͐����l���ݒ肳��Ă��܂��B���ꂼ��̔j���́A�ȉ��̔j���Ԃ�z�肷����̂ł��B
�@�ő�����Ђ��݃�t�E�E�E�����j��̊�F�R���N���[�g�ɂЂъ��ꂪ�傫���J�����
�@�ő刳�k�Ђ��݃Áfc�E�E�E���k�j��̊�F�R���N���[�g�����k�ωח͂��������
�@�ő傹��f�Ђ��݃�sh�E�E�E����f�j��̊�F�Ђъ���ʂ̂��ꂪ�傫���Ȃ���
������K�ɒ�߂邱�ƂŁA�j�[�h�̔�����\�ł��B�܂��A�����̊�͌v�Z�I���̔����Ƃ��Ȃ�܂��B�]���āA�����ꕔ�̗v�f���j���ɒB���Ă��v�Z���I�����Ă��܂��܂��̂ŁA�\���S�̂̌��E��Ԃ𐳂�������ł��Ȃ��ꍇ������܂��B���̂悤�ȍ\�����S�̌n�̌��E��Ԃ̔�����s�Ȃ��ꍇ�́A�j���l�𐄏��l���傫�߂ɐݒ肵�Ă����Ɨǂ��ꍇ������܂��B
|
| �@ |
|
| �p�R�|�P�P�D |
���ؗv�f�ƓS�ؔ�0.0��RC�v�f�́A���_�I�ɂ͓����ɂȂ�̂��H
�܂��A���l�̃��f���ŗ��҂���͂����ꍇ�A�v�Z���ʂɂǂ̂悤�ȈႢ��������̂��H |
| �`�R�|�P�P�D |
WCOMD�ł́A�u�S�̕t����p�̋y�ԗ̈�v��RC�v�f�A�����łȂ��̈�ؗv�f�Ƃ��邱�ƂŁA�\�����S�̂̉�͐��x�����߂邱�Ƃ��ł��܂��B
RC�v�f�Ɩ��ؗv�f�̈Ⴂ�́A���ɂЂъ��ꔭ����̈������͂̒ቺ���ARC�v�f�������ؗv�f�̂ق����傫���Ȃ邱�Ƃł��B���̈Ⴂ��\���p�����[�^�Ƃ��āA�g�����d��/��W���h��p���Ă��܂��B��{���[�h�ɂ����āARC�v�f�ł͈����d��/��W���FC=0.4�A���ؗv�f�ł͗v�f���@�Ɣj��G�l���M�[�ɉ����Ď����v�Z���A�ʏ�0.4�����傫���Ȃ�܂��B�]���āARC�v�f�ł͓S�ؔ��0�Ƃ��Ă�C��0.4���K�p����܂��̂ŁA���ؗv�f�Ɣ�ׂ�ƂЂъ��ꔭ����̈������͒ቺ�����ؗv�f�����������Ȃ�܂��B |
| �@ |
|
| �p�R�|�P�Q�D |
�o�͂����f�ʗ͓͂��������ŃK�E�X�_�̉��͂�p���ĎZ�肵�Ă���̂��H�o�͂����f�ʗ͂ƃK�E�X�_���͂Ƃ̑��ւ������Ăق����B |
| �`�R�|�P�Q�D |
���f�ʗ͂̎Z�o���@�ɂ���
�@UC-win/WCOMD�ł́A�f�ʗ͂��Z�o����ۂɐߓ_�͂��W�v���Ă��܂��BUC-win/Mesh�ɂ����āA�W�v�̑ΏۂƂȂ�ߓ_�����F�ŕ\������Ă��܂��B
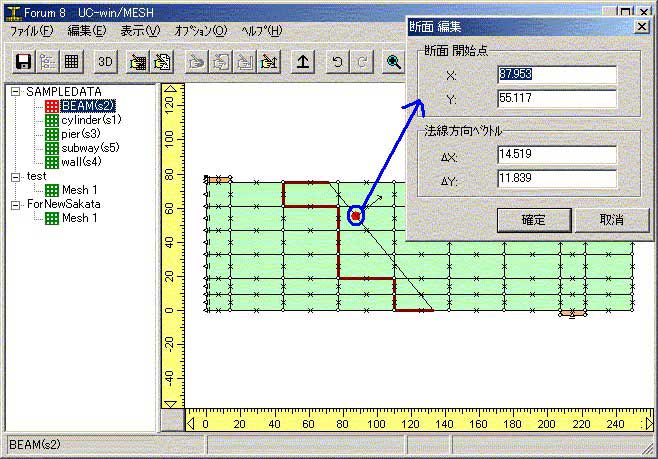
�]���āA�K�E�X�_�̉��͂��g�p���Ēf�ʗ͂��Z�o���Ă�����̂ł͂���܂���̂ł����ӂ��������B
�@�e�f�ʗ͂̕����̌����́A�ȉ��̂悤�ɂȂ��Ă��܂��B
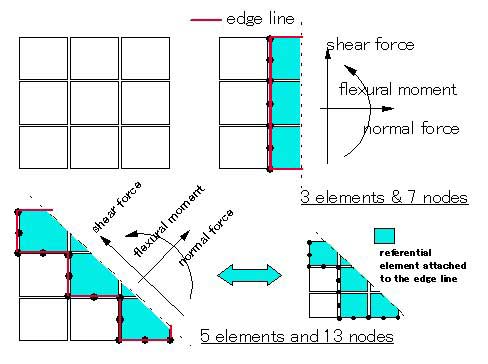
�@�@�@���́E�E�E�@���x�N�g���̌�������
�@�@�@����f�́E�E�E�ؒf�ʂɂ����č���������
�@�@�@�Ȃ����[�����g�E�E�E�ؒf�ʂɂ����č���肪�� |








