| Support Topics | ||
| サポートトピックス・FEM FEMLEEG | ||
|
||
|
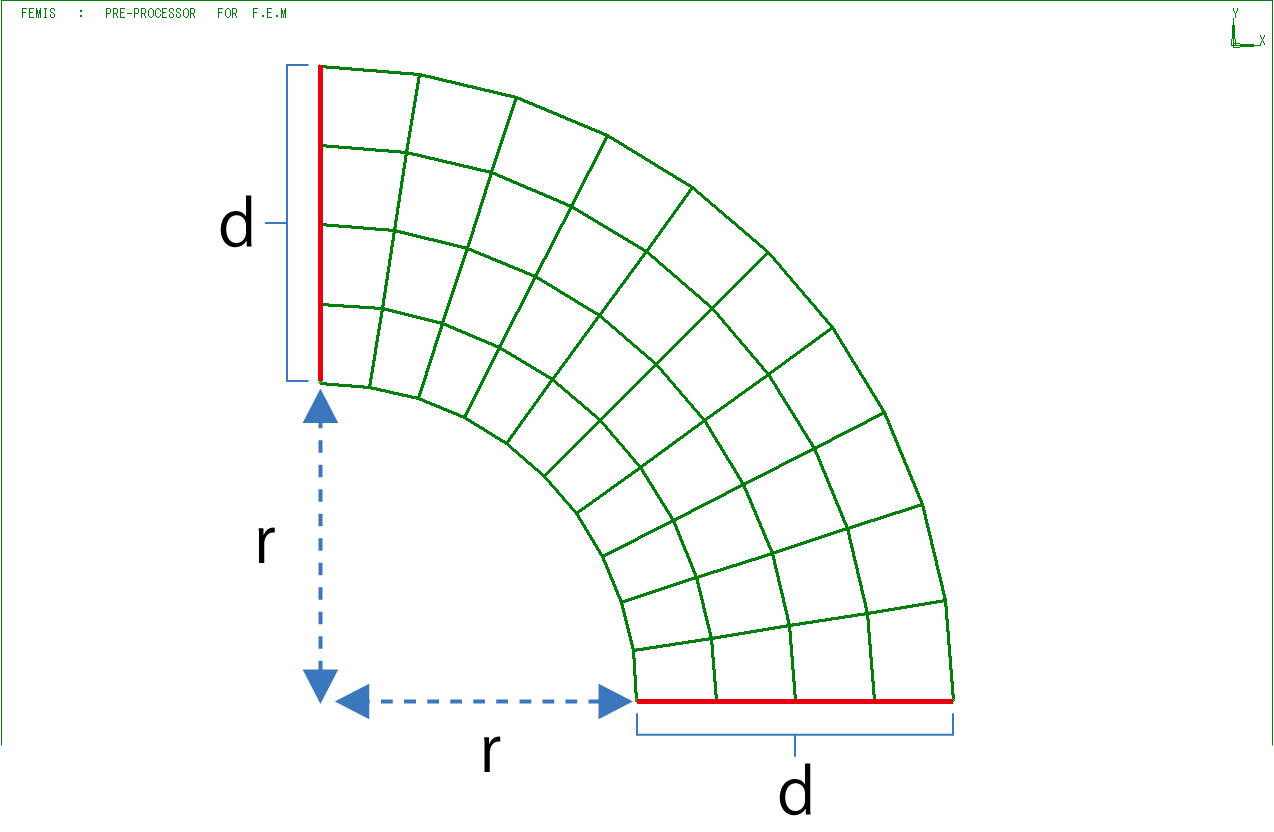
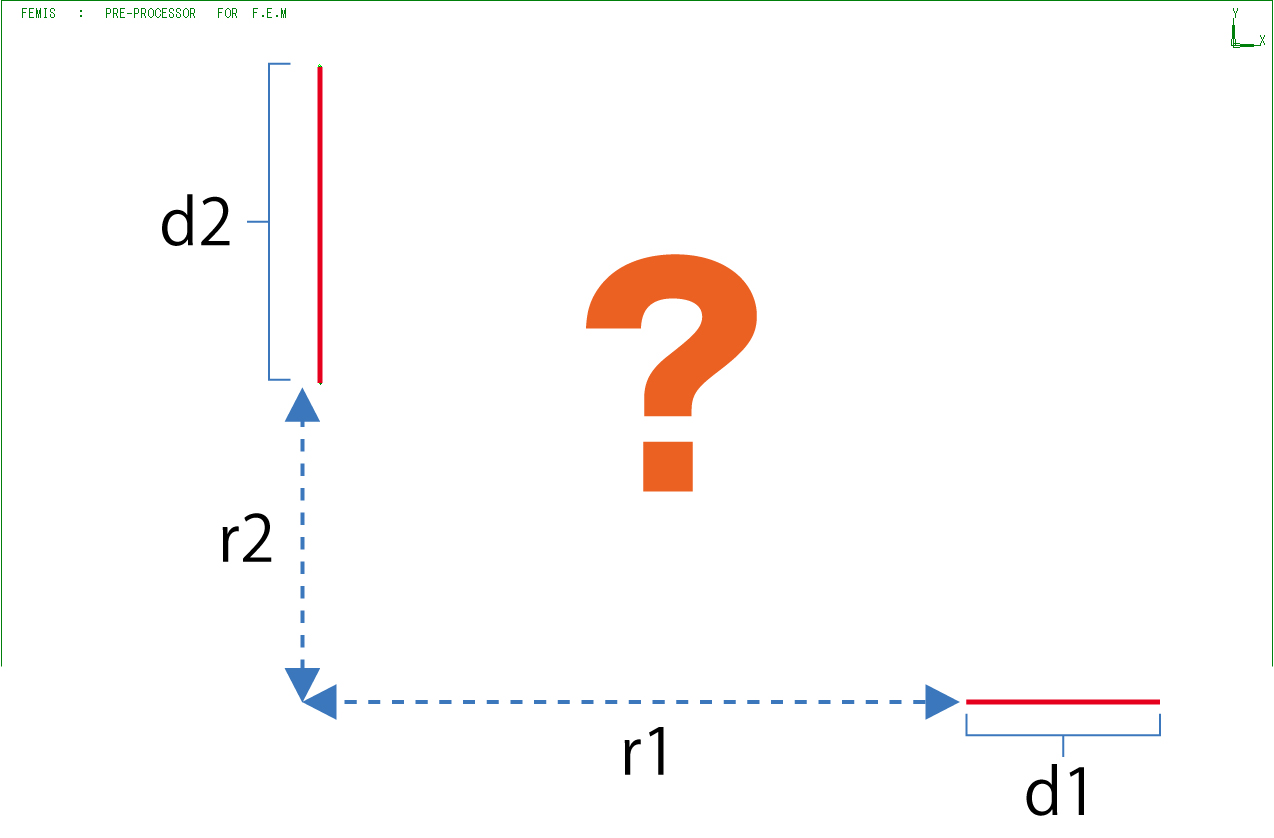
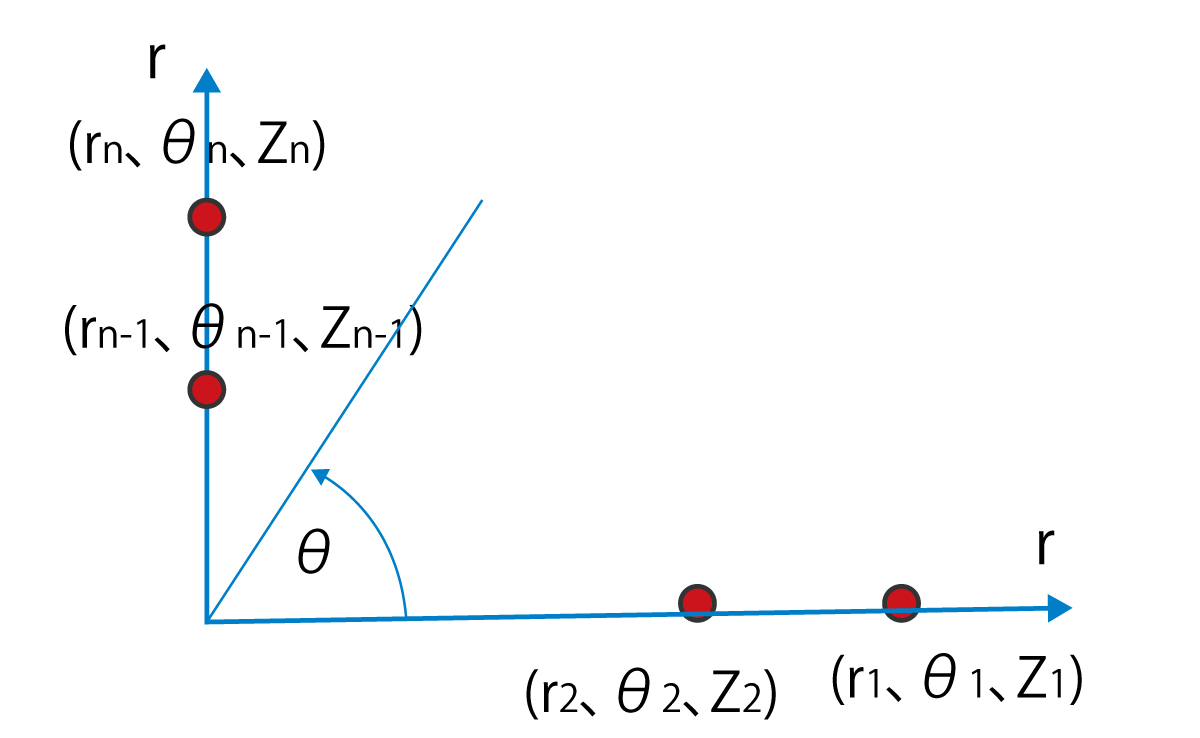
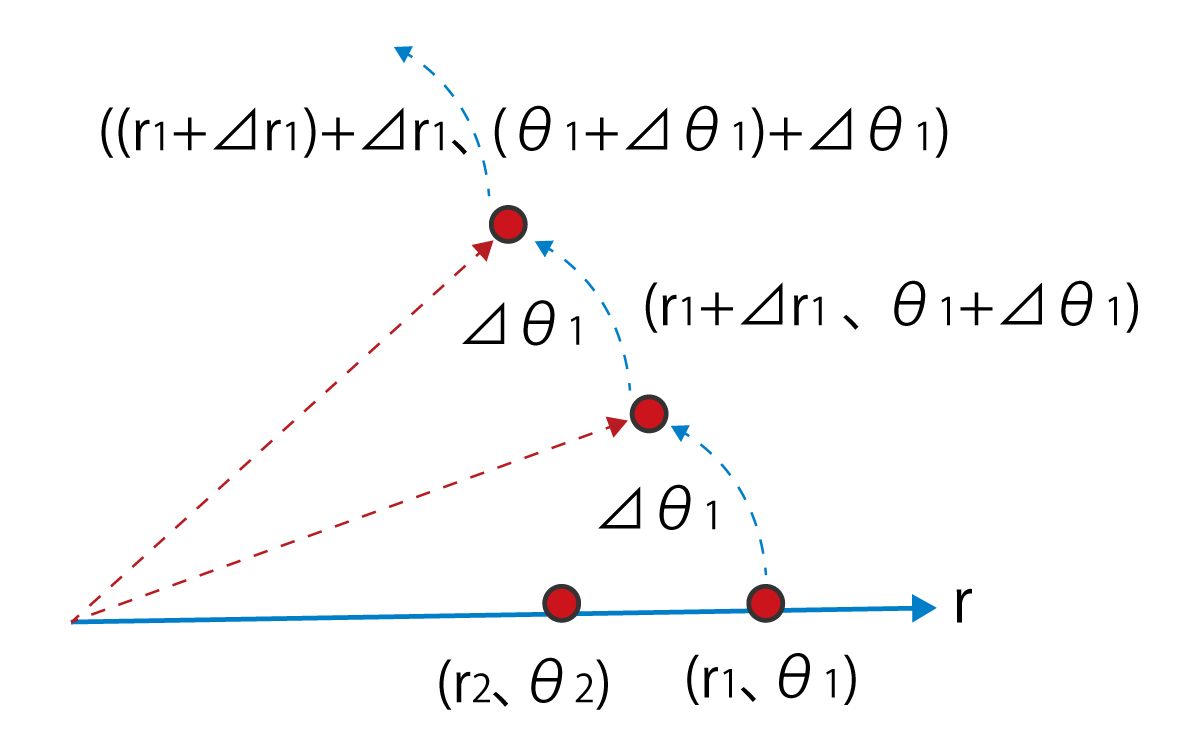
前回、円筒座標系を用いた面と面の結合で、開始と終了の断面の大きさが異なる、カーブしている3次元メッシュの生成を説明しました。 今回はその続きとして、メッシュがどのように円筒面上に補間されるか説明いたします。 面と面の結合 面と面の結合では、メッシュ数の関係は同じでなければなりません。開始と終了の面の大きさが異なる場合は相似の関係になっていることになります。 カーブをさせるには円筒座標系を指定します。指定した円筒座標系に沿ってメッシュを生成します。 ここで、同一サイズ、同一位置(円筒座標系では半径位置)にある面であれば図2のようになることは容易に想像がつきます。 では、面の大きさが異なったり、位置がずれている場合はどのようになるのでしょうか。 円筒座標系の面と面の結合のアルゴリズム 円筒座標系における面と面の結合の処理は以下の通りです。 1. 各面の節点座標値を直交座標系(x、y、z)から円筒座標系(r、θ、Z)の座標値に変換します。 2. 面の対応する節点の各座標値の差を分割数(m)で割った値を増分として求めます。 3. 開始面の各節点の座標値に成分ごとの増分を加算して次の節点座標とします。 4. 増分加算を繰り返して終了面までの節点を生成します。 これを開始面の全ての節点について行います。 5. 生成された節点から要素生成します。 |
(Up&Coming '24 盛夏号掲載)