はじめに

深礎基礎の降伏震度は、場所打ち杭のような杭基礎の降伏の目安から決まるものとは異なり、「上部構造の慣性力の作用位置での水平変位が急増し始めるとき」とされています。また水平荷重と水平変位の関係をlogP－logS法によるグラフから変位の急増点を読み取ることが、「斜面上の深礎基礎設計施工便覧　令和3年10月」(以降、深礎便覧と称します)に記載されています。

降伏震度の決定は設計者の判断に委ねられており、どのように決定するかについてのお問合せが多く寄せられています。

「深礎フレームの設計・3D配筋(部分係数法・H29道示対応)Ver.4」では、降伏震度を決定するための機能を追加しました。今回は新しい機能を使った降伏震度の算出方法についてご紹介いたします。

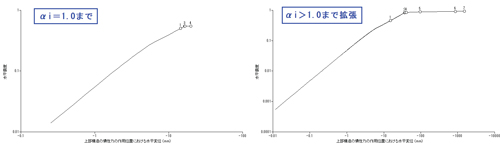
荷重増分の拡張

深礎便覧には、降伏変位を求めるための荷重増分方法として図1が示されています。

この方法は、khpによって荷重増分が頭打ちとなる場合に、載荷ステップαi＝1.0で荷重値が一致するように荷重増分の勾配を設定し、αi＝1.0以降も荷重増分の勾配を変えずに増加させています。

荷重増分を拡張することで、logP－logS法のグラフの範囲を広げ、変位急増点や基礎の降伏の目安を探せるようになります。

荷重増分を拡張しない場合とした場合での計算結果の違いの一例として図2を示します。

図2のαi＝1.0までの荷重増分（左図）では分かりにくかった変位急増点が、αi＞1.0まで計算した場合（右図）では明確になっています。このグラフから変位急増点が、想定した偶発作用時の荷重を超えた箇所で発生している場合は、「基礎は降伏しない」ということになります。

 

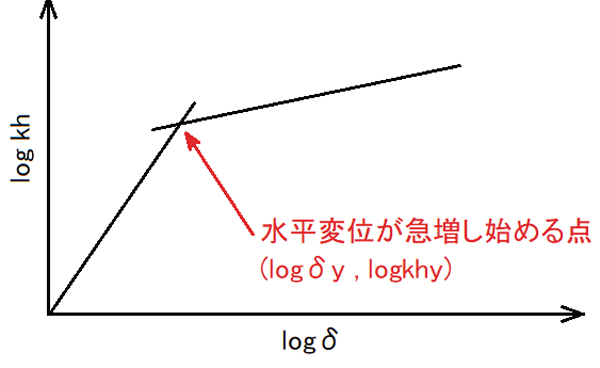
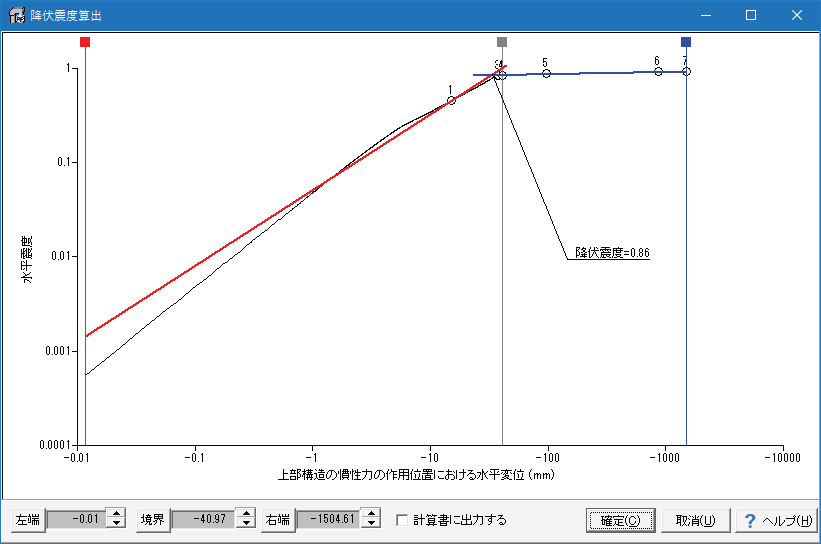
なお、この荷重増分方法は、αi＝1.0以下の範囲でもc2z・k2h0の荷重増分率が、元々の荷重増分率と異なるため、水平震度が同じでも同じ水平変位とはならないことにご注意ください。そのため、この荷重増分方法は、最終成果の部材照査などに用いるのものでは無く、降伏震度を求めるためのものとなります。

2つの直線が交差する点から降伏震度を求める

荷重増分の拡張で求めたlogP－logS法グラフを用いて２つの直線を設定し、その交点を降伏震度とします(図3)。

初期状態では、計算開始時の水平変位を左端、計算終了時（＝最後に計算した荷重増分時）の水平変位を右端とし、荷重増分単位で求めた変位急増点を境界として、左右２つの直線を最小二乗法で求めています。

 

グラフ部分にある３つの縦線は、２つの直線を求めるときのグラフのデータの範囲を指定するものです。それぞれの縦線は、縦線の上部にある■をマウスでドラッグするか、画面の下部にあるボタンを使って位置を変更することができます。

 

「荷重増分の拡張」と同様に、この画面で求められた降伏震度が偶発作用時の荷重を超えた箇所で発生している場合は、「基礎は降伏しない」ということになります。 このグラフは、計算書に出力することができますので、降伏震度決定の根拠として使用することができます。

 

※荷重増分の拡張グラフも計算書出力に対応しています。