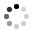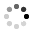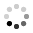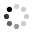連載 vol.2
オンライン麻雀サイト「天鳳」に見る暗号学的ハッシュ関数のしくみ
はじめまして。みるめも(https://mirumi.me)というブログをやっている みるみ といいます。本業はソフトウェアエンジニアで、毎日プログラムかブログを書いている…という人間です。しばらくの間、IT 技術を中心に幅広いネタで寄稿させていただくこととなりました。どうぞよろしくお願いいたします。
突然ですが、将棋と麻雀をそれぞれコンピュータ上で遊ぶことを考えてみます。私たちは不正のない公平なゲームを楽しむことを目的としていますが、残念ながらこの二種類のテーブルゲームのうち片方ではそれは難しいでしょう。両者の間にはある決定的な違いが存在しているからです。
それは私たちから見えない「舞台裏」があるかどうかです。将棋は盤面上に見えているすべての駒がゲームそのものであり、私たちが指す手以外に予測がつかないものは対戦相手の挙動だけです。しかしそこがゲームの本質ですから、これには何も問題はありません。
麻雀は違います。牌山の内容は全プレイヤーに対して伏せられており、次のツモで何を引くことになるかは誰にもわかりません。つまりここには舞台裏があり、私たちの知らない誰かが「うひひ、次のツモはこっそり差し替えてしまおう!」…と悪事を働けてしまうことを示唆しています。
これをソフトウェア、暗号学、および数学等の基本的な技術群によって解決を試みているのがオンライン麻雀サイト「天鳳」です。【画像1】
近年登場している麻雀対局サービスでも同様のアプローチが取られていることが多く、オンライン麻雀での公平性担保の先駆けといえるでしょう。
本記事では、天鳳がどのようにして不正がないことを証明しているかの「舞台裏」をご紹介いたします。
あらかじめ公開しておいてあとで答え合わせをする
問題解決の根本にあるのが「ハッシュ関数」という概念です。この目的と効果を理解するために、次のような問題に取り組んでみましょう。
アリスは2月14日にボブにラブレターを送ります。ただし、送付が遅れるのは避けたいため、ボブには少し早めにラブレターを送っておくことにしました。しかしこうすると、当然ですがボブは2月14日より前に開封して内容を確認することができてしまいます。つまり「ラブレターは渡しておくが告白の内容は2月14日まで明らかにしない方法」を考える必要がありそうです。
ここでハッシュ関数の登場です。ハッシュ関数は1つの入力と1つの出力を持っており、何かを入れると何かが出てくる自動販売機のようなものと捉えることができます。この自動販売機のルールは以下です。
- 入力したものとは一切関係のないでたらめな出力が返される
- 同じ入力に対しては必ずいつも同じ出力が返される
- 得られた出力から入力したものへと元に戻すことは絶対にできない
図にするとこのようなイメージになります。【画像2】
この作業をハッシュ化、もしくは単にハッシュするなどと言います。
ハッシュ関数がアリスのバレンタインデーをどのように解決するか見てみましょう。
アリスは、まずハッシュ化したメッセージを手紙に書いて2月14日より前にボブに到着するように送信します。この時点でボブはメッセージの内容を確認できますが、ルール3により元々書いてあった内容が何であったかを知ることはできません。そして2月14日を過ぎたら、アリスはボブに対して綴った告白のメッセージを「ボブの前でもう一度ハッシュ化してみせる」のです。ルール2により、同じ告白文なら必ず同じでたらめな出力が返されるので、ハッシュ化してみせた結果と既にボブに送信されていたメッセージとの一致を検証することによって「私が既に送っていたそのでたらめなメッセージは元々ラブレターだったんだよ!」ということを証明できるのです。もし1文字でも元のメッセージと異なるメッセージをハッシュ化した場合、ルール1により全く違う結果が出力されるので一致することはありません。
アリスは間違いなく2月14日の時点で告白をしたためたラブレターをボブに送信できていたことになります。
なんとも奇っ怪な愛の告白となりましたが、この流れは麻雀の牌山生成データの証明にもそのまま利用できそうな気がしませんか?
ハッシュ化された全ての牌山データが公開されている
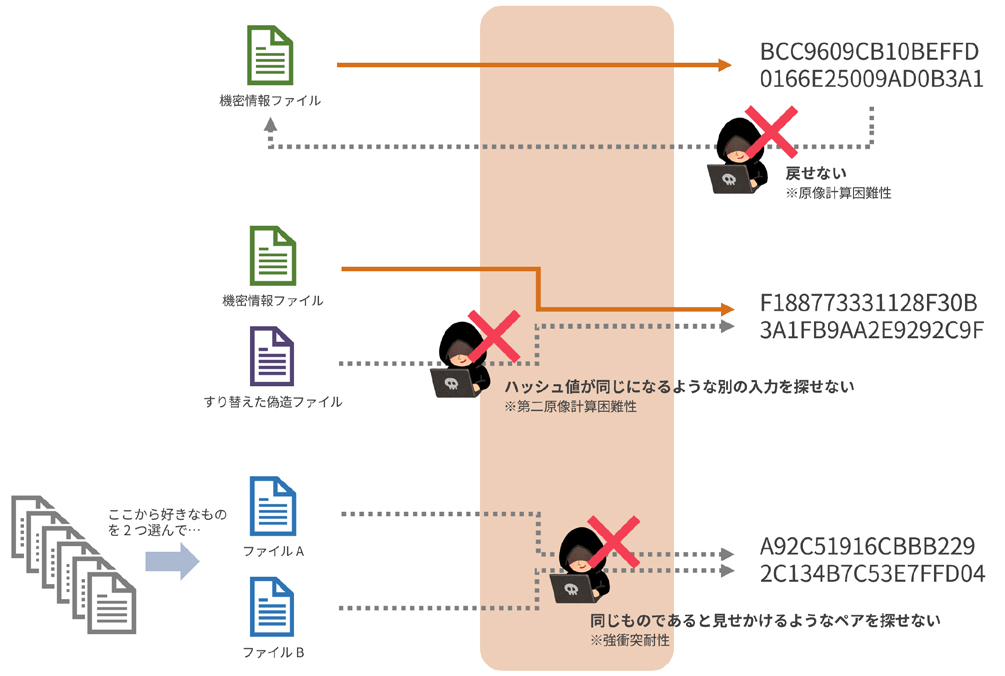
天鳳では、対局が始まる遥か以前より牌山が多数生成されており、かつそれがハッシュ化された状態で公開されています。対局が始まるごとにこの牌山プールから「消費」されていきます。【画像3】
3 こちら(https://tenhou.net/stat/rand/?00000-000b)から閲覧可能です。このページは「四般南喰赤」の卓用の牌山プールで、消費されるごとに左端の「USED」部分が付加されていくことも確認できます。
私たちは対局後、実際の牌譜データをもとに同じハッシュ操作を繰り返し、既に公開されていた牌山データと一致することをいつでも検証することができます。これすなわち、対局中にいかなる牌操作も行われていないことを随時証明できているということです。
生成された牌山がいつ誰に使われるかは全くわからないため、特定のプレイヤーに対して「積み込み」することも現実的に不可能でしょう(席順の問題もあります)。
より堅牢な暗号学的ハッシュ関数
ハッシュ関数について先ほどのアリスとボブの例では「ハッシュ化すると全くでたらめなデータが出力され、それを元に戻すことはできない」という基本的な部分のみを取り上げていました。しかし、セキュリティが重要視されるシーンでハッシュを利活用するにはもう一段階高いレベルのものを用いなければいけません。
これが「暗号学的ハッシュ関数」であり、次の3つの特性を持っているものとして定義されています。
- 原像計算困難性
- 第二原像計算困難性
- 強衝突耐性
前述の自動販売機のルールと一対一で対応しているわけではないことに注意してください。しいて言うならば、ルール3が特性Ⅰとの関連が強いです。それぞれの特性について簡単にご紹介します。
「原像計算困難性」は、主にハッシュ関数の基本的な性質である「一方向性」を指しています。あるハッシュされた値からもとのメッセージに戻すことがいかに難しいかを示す特性です。これはよくミキサーに例えられます。一度バラバラにしてしまったものは元に戻せないということですね。ただし注意するべきは、「技術的に極めて困難(非現実的)であるから無理だろう」という観点に基づいていることであり、途方もない時間とマシンパワーがあればこの特性は覆ってしまいます(他の二つの特性も同様ですし、現代の暗号技術にはほぼ全てこの考え方が当てはまります。「ミキサーで潰したりんごも、理論上は頑張れば元の形に戻せるよね?」と言っているようなものです)。
「第二原像計算困難性」は、あるハッシュ値と同じハッシュ値になるような別の入力を見つけることが困難でなければならないとする特性です。これは次に紹介する「強衝突耐性」と似ているのですが、基点となる入力とハッシュ値が決まっている場合に対する探索の困難性を説明している点で意味が異なります。
では「強衝突耐性」はというと、任意の2つの異なる入力で同じハッシュ値を持つような組み合わせを探すことはできないという特性です。こちらは、たとえ自由に入力のペアを選んでいい状況であったとしても同じハッシュ値になる(つまり衝突する)ものを探索するのは困難であるという意味合いです。「衝突困難性」とも呼ばれます。
これらの特性は、実際に攻撃を行う立場になってみると非常に理解しやすくなります。【画像4】
天鳳で採用されている暗号学的ハッシュ関数は「SHA-512」というもので、これは代表的な暗号学的ハッシュ関数のひとつです。中でも特にセキュリティ的に堅牢であるとされています。
実はこの様子も公開されていて、こちら(http://blog.tenhou.net/article/30503297.html)から確認ができます。掲載されているプログラムのコード内からもSHA-512が使用されていることが伺えますね(このソースコード内に登場する SHA-512 は実際には後述するランダム処理に使われているものですが、生成結果の牌山に対しても同様にSHA-512を使用している旨がここ(https://tenhou.net/stat/rand/)で言及されています)。
そもそもの牌山生成はちゃんと「混ざって」いるのか
牌山の生成以降に起き得る問題については解決できましたから、最後に「そもそも十分にランダムな牌山生成が行われているか」についても触れておきましょう。
麻雀というゲームへの参加者の視点から考えると、自分にツキがないときに疑いたくなるのはどちらかというと牌操作よりも「ちゃんとランダムに混ざってる!?」という感覚ではないでしょうか。事実、コンピュータは元来ランダムという概念と相性が非常に悪く、ソフトウェアだけで「何もないところから真にランダムな結果を生成しつづけること」はとても難しいです。
これを解決するため、現代のCPU周辺アーキテクチャにはデバイスの熱ノイズなどから真にランダムなエントロピーを取得できる「ハードウェア乱数生成器」と呼ばれるものが備わるようになりました。また、ユーザーがマウスを動かす軌跡などを利用してOSレベルで乱数生成するようなAPIも一般的であり、例えば WindowsのCryptGenRandom 関数はその代表例です。
ここで生成された強力なランダム出力をもとにして、ソフトウェア上で手軽に実行できるランダム関数(擬似乱数生成器といいます)の入力として使います。…という流れも、実は先ほど掲載した牌山生成アルゴリズム内にやはり明確に記述があります。
まとめますと、「入力と出力の関係および規則性が全く予期できない、かつ十分に撹拌されたランダム処理によって牌山は生成されている」ということになります。
しかしどんなに技術的に証明されているとはいえ、やはり納得のいかない対局はたくさんありますよね。理屈を知っているだけにより悶々としてしまう筆者でした。
(執筆:みるみ)

(Up&Coming '23 秋の号掲載)
|
||||||||
 Up&Coming |